Line graph

This article is about the mathematical concept. For statistical presentation method, see line chart.

In graph theory, the line graph L(G) of undirected graph G is another graph L(G) that represents the adjacencies between edges of G. The name line graph comes from a paper by Harary & Norman (1960) although both Whitney (1932) and Krausz (1943) used the construction before this.^[1] Other terms used for the line graph include edge graph,^[2] the theta-obrazom,^[3] the covering graph,^[3] the derivative,^[3] the edge-to-vertex dual,^[3] the interchange graph,^[2] the adjoint graph,^[2] the conjugate,^[3] the derived graph,^[2] and the representative graph.^[3]

One of the earliest and most important theorems about line graphs is due to Hassler Whitney (1932), who proved that with one exceptional case the structure of G can be recovered completely from its line graph. In other words, with that one exception, the entire graph can be deduced from knowing the adjacencies of edges ("lines").

Formal definition

Given a graph G, its line graph L(G) is a graph such that

• each vertex of L(G) represents an edge of G; and
• two vertices of L(G) are adjacent if and only if their corresponding edges share a common endpoint ("are adjacent") in G.

That is, it is the intersection graph of the edges of G, representing each edge by the set of its two endpoints.

Examples

Example construction

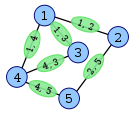
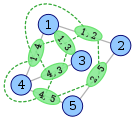
The following figures show a graph (left, with blue vertices) and its line graph (right, with green vertices). Each vertex of the line graph is shown labeled with the pair of endpoints of the corresponding edge in the original graph. For instance, the green vertex on the right labeled 1,3 corresponds to the edge on the left between the blue vertices 1 and 3. Green vertex 1,3 is adjacent to three other green vertices: 1,4 and 1,2 (corresponding to edges sharing the endpoint 1 in the blue graph) and 4,3 (corresponding to an edge sharing the endpoint 3 in the blue graph).

• 

  Graph G

• 

  Vertices in L(G) constructed from edges in G

• 

  Added edges in L(G)

• 

  The line graph L(G)

Line graphs of convex polyhedra

A source of examples from geometry are the line graphs of the graphs of simple polyhedra. Taking the line graph of the graph of the tetrahedron one gets the graph of the octahedron; from the graph of the cube one gets the graph of a cuboctahedron; from the graph of the dodecahedron one gets the graph of the icosidodecahedron, etc. Geometrically, the operation consists in cutting each vertex of the polyhedron with a plane cutting all edges adjacent to the vertex at their midpoints; it is sometimes named rectification.

If a polyhedron is not simple (it has more than three edges at a vertex) the line graph will be nonplanar, with a clique replacing each high-degree vertex. The medial graph is a variant of the line graph of a planar graph, in which two vertices of the medial graph are adjacent if and only if the corresponding two edges are consecutive on some face of the planar graph. For simple polyhedra, the medial graph and the line graph coincide, but for non-simple graphs the medial graph remains planar. Thus, the medial graphs of the cube and octahedron are both isomorphic to the graph of the cuboctahedron, and the medial graphs of the dodecahedron and icosahedron are both isomorphic to the graph of the icosidodecahedron.

Properties

Properties of a graph G that depend only on adjacency between edges may be translated into equivalent properties in L(G) that depend on adjacency between vertices. For instance, a matching in G is a set of edges no two of which are adjacent, and corresponds to a set of vertices in L(G) no two of which are adjacent, that is, an independent set.

Thus,

• The line graph of a connected graph is connected. If G is connected, it contains a path connecting any two of its edges, which translates into a path in L(G) containing any two of the vertices of L(G). However, a graph G that has some isolated vertices, and is therefore disconnected, may nevertheless have a connected line graph.
• A maximum independent set in a line graph corresponds to maximum matching in the original graph. Since maximum matchings may be found in polynomial time, so may the maximum independent sets of line graphs, despite the hardness of the maximum independent set problem for more general families of graphs.
• The edge chromatic number of a graph G is equal to the vertex chromatic number of its line graph L(G).
• The line graph of an edge-transitive graph is vertex-transitive.
• If a graph G has an Euler cycle, that is, if G is connected and has an even number of edges at each vertex, then the line graph of G is Hamiltonian. (However, not all Hamiltonian cycles in line graphs come from Euler cycles in this way.)
• Line graphs are claw-free graphs, graphs without an induced subgraph in the form of a three-leaf tree.
• The line graphs of trees are exactly the claw-free block graph.

Characterization and recognition

The nine minimal non-line graphs, from Beineke's forbidden-subgraph characterization of line graphs. A graph is a line graph if and only if it does not contain one of these nine graphs as an induced subgraph.

A graph G is the line graph of some other graph, if and only if it is possible to find a collection of cliques in G, partitioning the edges of G, such that each vertex of G belongs to exactly two of the cliques. In order to do this, it may be necessary for some of the cliques to be single vertices. By the result of Whitney (1932),^[4] if G is not a triangle, there can be only one partition of this type. If such a partition exists, we can recover the original graph for which G is a line graph, by creating a vertex for each clique, and connecting two cliques by an edge whenever G contains a vertex belonging to both cliques. Therefore, except for the case of K₃ and K_1,3, if the line graphs of two connected graphs are isomorphic then the graphs are isomorphic. Roussopoulos (1973) used this observation as the basis for a linear time algorithm for recognizing line graphs and reconstructing their original graphs.

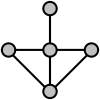
For example, this characterization can be used to show that the following graph is not a line graph:

In this example, the edges going upward, to the left, and to the right from the central degree-four vertex do not have any cliques in common. Therefore, any partition of the graph's edges into cliques would have to have at least one clique for each of these three edges, and these three cliques would all intersect in that central vertex, violating the requirement that each vertex appear in exactly two cliques. Thus, the graph shown is not a line graph.

An alternative characterization of line graphs was proven by Beineke 1970 (first reported without proof in Beineke (1968)). He showed that there are nine minimal graphs that are not line graphs, such that any graph that is not a line graph has one of these nine graphs as an induced subgraph. That is, a graph is a line graph if and only if no subset of its vertices induces one of these nine graphs. In the example above, the four topmost vertices induce a claw (that is, a complete bipartite graph K_1,3), shown on the top left of the illustration of forbidden subgraphs. Therefore, by Beineke's characterization, this example cannot be a line graph. For graphs with minimum degree at least 5, only the six subgraphs in the left and right columns of the figure are needed in the characterization.^[5] This result in Metelsky et al. is similar to the results of Line graphs of hypergraphs.^[6]

Iterating the line graph operator

van Rooij & Wilf (1965) consider the sequence of graphs

$G, L(G), L(L(G)), L(L(L(G))), \dots.\$

They show that, when G is a finite connected graph, only four possible behaviors are possible for this sequence:

• If G is a cycle graph then L(G) and each subsequent graph in this sequence is isomorphic to G itself. These are the only connected graphs for which L(G) is isomorphic to G.
• If G is a claw K_1,3, then L(G) and all subsequent graphs in the sequence are triangles.
• If G is a path graph then each subsequent graph in the sequence is a shorter path until eventually the sequence terminates with an empty graph.
• In all remaining cases, the sizes of the graphs in this sequence eventually increase without bound.

If G is not connected, this classification applies separately to each component of G.

Relations to other families of graphs

Every line graph is a claw-free graph. Some of the properties of claw-free graphs are generalizations of those of line graphs.

The line graph of a bipartite graph is perfect (see König's theorem). The line graphs of bipartite graphs form one of the key building blocks of perfect graphs, used in the proof of the perfect graph theorem. A special case is the rook's graphs, line graphs of complete bipartite graphs.

Generalizations

Multigraphs

The concept of the line graph of G may naturally be extended to the case where G is a multigraph, although in that case Whitney's uniqueness theorem no longer holds; for instance a complete bipartite graph K_1,n has the same line graph as the dipole graph and Shannon multigraph with the same number of edges.

Line digraphs

It is also possible to generalize line graphs to directed graphs.^[7] If G is a directed graph, its directed line graph or line digraph has one vertex for each edge of G. Two vertices representing directed edges from u to v and from w to x in G are connected by an edge from uv to wx in the line digraph when v = w. That is, each edge in the line digraph of G represents a length-two directed path in G. The de Bruijn graphs may be formed by repeating this process of forming directed line graphs, starting from a complete directed graph.^[8]

Weighted line graphs

In a line graph L(G), each vertex of degree k in the original graph G creates k(k-1)/2 edges in the line graph. For many types of analysis this means high degree nodes in G are over represented in the line graph L(G). For instance consider a random walk on the vertices of the original graph G. This will pass along some edge e with some frequency f. On the other hand this edge e is mapped to a unique vertex, say v, in the line graph L(G). If we now perform the same type of random walk on the vertices of the line graph, the frequency with which v is visited can be completely different from f. If our edge e in G was connected to nodes of degree O(k), it will be traversed O(k²) more frequently in the line graph L(G). Put another way, Whitney's theorem (Whitney (1932)) guarantees that the line graph almost always encodes the topology of the original graph G faithfully but it does not guarantee that dynamics on these two graphs have a simple relationship. One solution is to construct a weighted line graph, that is, a line graph with weighted edges. There are several natural ways to do this (Evans & Lambiotte 2009). For instance if edges d and e in the graph G are incident at a vertex v with degree k, then in the line graph L(G) the edge connecting the two vertices d and e can be given weight 1/(k-1). In this way every edge in G (provided neither end is connected to a vertex of degree '1') will have strength 2 in the line graph L(G) corresponding to the two ends that the edge has in G.

Line graphs of hypergraphs

The edges of a hypergraph may form an arbitrary family of sets, so the line graph of a hypergraph is the same as the intersection graph of the sets from the family.

Notes

1. ^ Hemminger & Beineke (1978, p. 273).
2. ^ ^{a b c d} Balakrishnan (1997, p. 44)
3. ^ ^{a b c d e f} Hemminger & Beineke (1978, pp. 273)
4. ^ See also Krausz (1943).
5. ^ Metelsky & Tyshkevich (1997).
6. ^ Weisstein, Eric W., "Line Graph" from MathWorld.
7. ^ Harary, Frank, and Norman, Robert Z., "Some properties of line digraphs", Rend. Circ. Mat. Palermo, II. Ser. 9 (1960), 161-168.
8. ^ Zhang & Lin (1987).

References

• Balakrishnan, V. K. (1997), Schaum's Outline of Graph Theory (1st ed.), McGraw-Hill, ISBN 0070054894 .
• Beineke, L. W. (1968), "Derived graphs of digraphs", in Sachs, H.; Voss, H.-J.; Walter, H.-J., Beiträge zur Graphentheorie, Leipzig: Teubner, pp. 17–33 .
• Beineke, L. W. (1970), "Characterizations of derived graphs", Journal of Combinatorial Theory 9 (2): 129–135, doi:10.1016/S0021-9800(70)80019-9, MR0262097 .
• Brandstädt, Andreas; Le, Van Bang; Spinrad, Jeremy P. (1999), Graph Classes: A Survey, SIAM Monographs on Discrete Mathematics and Applications, ISBN 0-89871-432-X .
• Evans, T.S.; Lambiotte, R. (2009), "Line Graphs, Link Partitions and Overlapping Communities", Phys.Rev.E 80: 016105, doi:10.1103/PhysRevE.80.016105 .
• Harary, F.; Norman, R. Z. (1960), "Some properties of line digraphs", Rendiconti del Circolo Matematico di Palermo 9 (2): 161–169, doi:10.1007/BF02854581 .
• Hemminger, R. L.; Beineke, L. W. (1978), "Line graphs and line digraphs", in Beineke, L. W.; Wilson, R. J., Selected Topics in Graph Theory, Academic Press Inc., pp. 271–305 .
• Krausz, J. (1943), "Démonstration nouvelle d'un théorème de Whitney sur les réseaux", Mat. Fiz. Lapok 50: 75–85, MR0018403 .
• Metelsky, Yury; Tyshkevich, Regina (1997), "On line graphs of linear 3-uniform hypergraphs", Journal of Graph Theory 25 (4): 243–251, doi:10.1002/(SICI)1097-0118(199708)25:4<243::AID-JGT1>3.0.CO;2-K .
• van Rooij, A. C. M.; Wilf, H. S. (1965), "The interchange graph of a finite graph", Acta Mathematica Hungarica 16 (3–4): 263–269, doi:10.1007/BF01904834 .
• Roussopoulos, N. D. (1973), "A max {m,n} algorithm for determining the graph H from its line graph G", Information Processing Letters 2 (4): 108–112, doi:10.1016/0020-0190(73)90029-X, MR0424435 .
• Whitney, H. (1932), "Congruent graphs and the connectivity of graphs", American Journal of Mathematics 54 (1): 150–168, doi:10.2307/2371086, JSTOR 2371086 .
• Zhang, Fu Ji; Lin, Guo Ning (1987), "On the de Bruijn–Good graphs", Acta Math. Sinica 30 (2): 195–205, MR0891925 .

External links

• line graphs, Information System on Graph Class Inclusions, http://wwwteo.informatik.uni-rostock.de/isgci/classes/gc_249.html