- Golomb ruler
-
"OGR" redirects here. For the OGR programming library, see GDAL.
 Golomb ruler of order 4 and length 6. This ruler is both optimal and perfect.
Golomb ruler of order 4 and length 6. This ruler is both optimal and perfect.In mathematics, a Golomb ruler is a set of marks at integer positions along an imaginary ruler such that no two pairs of marks are the same distance apart. The number of marks on the ruler is its order, and the largest distance between two of its marks is its length. Translation and reflection of a Golomb ruler are considered trivial, so the smallest mark is customarily put at 0 and the next mark at the smaller of its two possible values.
The Golomb ruler was named for Solomon W. Golomb and discovered independently by Sidon[1] and Babcock.[2]
There is no requirement that a Golomb ruler be able to measure all distances up to its length, but if it does, it is called a perfect Golomb ruler. It has been proven that no perfect Golomb ruler exists for five or more marks.[3] A Golomb ruler is optimal if no shorter Golomb ruler of the same order exists. Creating Golomb rulers is easy, but finding the optimal Golomb rulers for a specified order is computationally very challenging. Distributed.net has completed distributed massively parallel searches for optimal order-24,[4] order-25[5] and order-26[6][7] Golomb rulers, confirming the suspected candidates.[8][9] Distributed.net also has plans to find optimal Golomb rulers (OGRs) of order-27 and order-28. However, they are not expected to take as long as the previous projects due to the discovery of an improved algorithm.[10] Distributed.net is actively searching for the optimal order-27 ruler; in May 2009, the expected time to discover it was estimated at about seven years.[11] As of September 2011[update], the computation was about 43% complete, after 940 days (2.5 years) of work.[12]
Currently, the complexity of finding OGRs of arbitrary order n (where n is given in unary) is unknown. In the past there was some speculation that it is an NP-hard problem.[3] Problems related to the construction of Golomb Rulers are provably shown to be NP-hard, where it is also noted that no known NP-complete problem has similar flavor to finding Golomb Rulers.[13]
Contents
Definitions
Golomb rulers as sets
A set of integers

is a Golomb ruler if and only if
 [14]
[14]The order of such a Golomb ruler is m and its length is am − a1. The canonical form has a1 = 0 and, if m > 2, a2 − a1 < am − am − 1. Such a form can be achieved through translation and reflection.
Golomb rulers as functions

with f(1) = 0 and f(m) = n is a Golomb ruler if and only if
 [15]:236
[15]:236The order of such a Golomb ruler is m and its length is n. The canonical form has
- f(2) < f(m) − f(m − 1) if m > 2.
Optimality
A Golomb ruler of order m with length n may be optimal in either of two respects:[15]:237
- it may be optimally dense, exhibiting maximal m for the specific value of n
- it may be optimally short, exhibiting minimal n for the specific value of m
The general term optimal Golomb ruler is used to refer to the second type of optimality.
Practical Applications
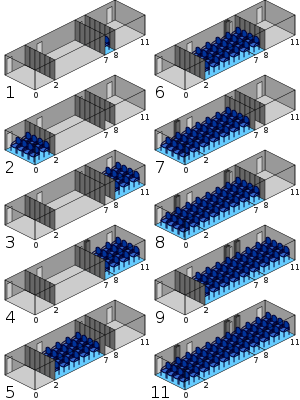 Example of a conference room with proportions of a [0, 2, 7, 8, 11] Golomb ruler, making it configurable to 10 different sizes.[16]
Example of a conference room with proportions of a [0, 2, 7, 8, 11] Golomb ruler, making it configurable to 10 different sizes.[16]
Information Theory/Error Correction
Golomb rulers are used within Information Theory related to error correcting codes.[17]
Radio Frequency Selection
Golomb rulers are used in the selection of radio frequencies to reduce the effects of intermodulation interference with both terrestrial[18] and extraterrestrial[19] applications.
Radio Antennae Placement
Golomb rulers are used in the design of phased array radio antennas such as radio telescopes. Antennas in a [0,1,4,6] Golomb ruler configuration can often be seen at cell sites.[dubious ]
Methods of construction
A number of construction methods produce asymptotically optimal Golomb rulers.
Erdős–Turan construction
The following construction, due to Paul Erdős and Pál Turán, produces a Golomb ruler for every odd prime p.[20]
![2pk+(k^2\,\bmod\,p),k\in[0,p-1]](4/b24d357139b6cea59071524fedc39657.png)
Known optimal Golomb rulers
The following table contains all known optimal Golomb rulers, excluding those with marks in the reverse order. The first four are perfect.
order length marks 1 0 0 2 1 0 1 3 3 0 1 3 4 6 0 1 4 6 5 11 0 1 4 9 11
0 2 7 8 116 17 0 1 4 10 12 17
0 1 4 10 15 17
0 1 8 11 13 17
0 1 8 12 14 177 25 0 1 4 10 18 23 25
0 1 7 11 20 23 25
0 1 11 16 19 23 25
0 2 3 10 16 21 25
0 2 7 13 21 22 258 34 0 1 4 9 15 22 32 34 9 44 0 1 5 12 25 27 35 41 44 10 55 0 1 6 10 23 26 34 41 53 55 11 72 0 1 4 13 28 33 47 54 64 70 72
0 1 9 19 24 31 52 56 58 69 7212 85 0 2 6 24 29 40 43 55 68 75 76 85 13 106 0 2 5 25 37 43 59 70 85 89 98 99 106 14 127 0 4 6 20 35 52 59 77 78 86 89 99 122 127 15 151 0 4 20 30 57 59 62 76 100 111 123 136 144 145 151 16 177 0 1 4 11 26 32 56 68 76 115 117 134 150 163 168 177 17 199 0 5 7 17 52 56 67 80 81 100 122 138 159 165 168 191 199 18 216 0 2 10 22 53 56 82 83 89 98 130 148 153 167 188 192 205 216 19 246 0 1 6 25 32 72 100 108 120 130 153 169 187 190 204 231 233 242 246 20 283 0 1 8 11 68 77 94 116 121 156 158 179 194 208 212 228 240 253 259 283 21 333 0 2 24 56 77 82 83 95 129 144 179 186 195 255 265 285 293 296 310 329 333 22 356 0 1 9 14 43 70 106 122 124 128 159 179 204 223 253 263 270 291 330 341 353 356 23 372 0 3 7 17 61 66 91 99 114 159 171 199 200 226 235 246 277 316 329 348 350 366 372 24 425 0 9 33 37 38 97 122 129 140 142 152 191 205 208 252 278 286 326 332 353 368 384 403 425 25 480 0 12 29 39 72 91 146 157 160 161 166 191 207 214 258 290 316 354 372 394 396 431 459 467 480 26 492 0 1 33 83 104 110 124 163 185 200 203 249 251 258 314 318 343 356 386 430 440 456 464 475 487 492 See also
- Costas array
- Sparse ruler
- Perfect ruler
- Sidon sequence
References
- ^ S. Sidon, "Ein Satz über trigonometrische Polynome und seine Anwendungen in der Theorie der Fourier-Reihen", Mathematische Annalen 106 (1932), pp. 536–539
- ^ Wallace C. Babcock. "Intermodulation Interference in Radio Systems/Frequency of Occurrence and Control by Channel Selection", Bell System Technical Journal 31 (1953), pp. 63–73.
- ^ a b "Modular and Regular Golomb Rulers". http://cgm.cs.mcgill.ca/~athens/cs507/Projects/2003/JustinColannino.
- ^ "stats.distributed.net - OGR-24 Overall Project Stats". http://stats.distributed.net/projects.php?project_id=24. Retrieved 2008-03-27.
- ^ "stats.distributed.net - OGR-25 Overall Project Stats". http://stats.distributed.net/projects.php?project_id=25. Retrieved 2008-09-22.
- ^ http://n0cgi.distributed.net/cgi/planarc.cgi?user=bovine
- ^ http://www.distributed.net/projects.php
- ^ "distributed.net - .plan archives". http://n0cgi.distributed.net/cgi/planarc.cgi?user=nugget&plan=2004-11-01.10:24. Retrieved 2008-03-27.
- ^ "distributed.net - .plan archives 2". http://n0cgi.distributed.net/cgi/planarc.cgi?user=bovine&plan=2008-10-25.23:14. Retrieved 2008-10-26.
- ^ http://n0cgi.distributed.net/cgi/planarc.cgi?user=bovine&plan=2008-10-26.09:52
- ^ bovine's plan, 24-Feb-2009 17:26
- ^ OGR-27 / Overall Project Stats
- ^ C. Meyer, P.A. Papakonstantinou, "On the Complexity of Constructing Golomb Rulers". http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6TYW-4T9TBYY-2&_user=10&_rdoc=1&_fmt=&_orig=search&_sort=d&view=c&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=202862ee62742f681c1cb98244414dc4., Discrete Applied Mathematics
- ^ Dimitromanolakis, Apostolos (PDF). Analysis of the Golomb Ruler and the Sidon Set Problems, and Determination of Large, Near-Optimal Golomb Rulers. http://www.cs.toronto.edu/%7Eapostol/golomb/main.pdf. Retrieved 2009-12-20.
- ^ a b Drakakis, Konstantinos (2009). "A Review Of The Available Construction Methods For Golomb Rulers". Advances in Mathematics of Communications 3 (3): 235–250. doi:10.3934/amc.2009.3.235.
- ^ Paul Erdos and P. Turan. "On a problem of Sidon in additive number theory, and on some related problems," J. London Math. Soc, 16:212--215, 1941
- ^ "A class of binary recurrent codes with limited error propagation" (abstract). http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=1053951. Retrieved 2011-03-14.
- ^ "Intermodulation Interference in Radio Systems" (excerpt). http://www.alcatel-lucent.com/bstj/vol32-1953/articles/bstj32-1-63.pdf. Retrieved 2011-03-14.
- ^ "Carrier frequency assignment for nonlinear repeaters" (abstract). Bibcode 1977COMTR...7..227F.
- ^ Erdős, Paul; Turán, Pál (1941). "On a problem of Sidon in additive number theory and some related problems". Journal of the London Mathematical Society 16 (4): 212–215. doi:10.1112/jlms/s1-16.4.212.
- Gardner, Martin (March 1972). "Mathematical games". Scientific American: 108–112.
External links
Categories:- Number theory
- Antennas (radio)
Wikimedia Foundation. 2010.
