Dodecahedral prism

Dodecahedral prism
Schlegel diagram Only one dodecahedral cell shown
Type	Prismatic uniform polychoron
Uniform index	57
Schläfli symbol	{5,3}x{}
Coxeter-Dynkin
Cells	2 (5.5.5) 12 (4.4.5)
Faces	30 {4} 24 {5}
Edges	80
Vertices	40
Vertex configuration	Equilateral-triangular pyramid
Symmetry group	[5,3,2], order 240
Properties	convex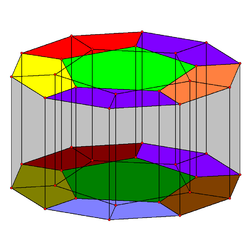

Transparent Schlegel diagram

An orthographic projection with a wireframe model and has half of the pentagonal faces colored to show the two dodecahedra. The dodecahedra are regular, but look flattened because of the projection and direction of viewing.

In geometry, a dodecahedral prism is a convex uniform polychoron (four dimensional polytope). This polychoron has 14 polyhedral cells: 2 dodecahedra connected by 12 pentagonal prisms. It has 54 faces: 30 squares and 24 pentagons. It has 80 edges and 40 vertices.

It can be constructed by creating two coinciding dodecahedra in 3-space, and translating each copy in opposite perpendicular directions in 4-space until their separation equals their edge length.

Alternative names:

1. Dodecahedral dyadic prism Norman W. Johnson
2. Dope (for dodecahedral prism) Jonathan Bowers
3. Dodecahedral hyperprism

It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids or Archimedean solids.

Structure

The dodecahedral prism consists of two dodecahedra connected to each other via 12 pentagonal prisms. The pentagonal prisms are joined to each other via their square faces.

Projections

The pentagonal-prism-first orthographic projection of the dodecahedral prism into 3D space has a decagonal envelope (see diagram). Two of the pentagonal prisms project to the center of this volume, each surrounded by 5 other pentagonal prisms. They form two sets (each consisting of a central pentagonal prism surrounded by 5 other non-uniform pentagonal prisms) that cover the volume of the decagonal prism twice. The two dodecahedra project onto the decagonal faces of the envelope.

The dodecahedron-first orthographic projection of the dodecahedral prism into 3D space has a dodecahedral envelope. The two dodecahedral cells project onto the entire volume of this envelope, while the 12 decagonal prismic cells project onto its 12 pentagonal faces.

External links

• 6. Convex uniform prismatic polychora - Model 57, George Olshevsky.
• Richard Klitzing, 4D uniform polytopes (polychora), x o3o5x - dope

This polyhedron-related article is a stub. You can help Wikipedia by expanding it.v · Categories: Four-dimensional geometry Polychora Polyhedron stubs Wikimedia Foundation. 2010. Игры ⚽ Поможем написать реферат Eduardo Macia Ragnar Stenberg Look at other dictionaries: Prism (geometry) — For other uses, see Prism (disambiguation). Set of uniform prisms (A hexagonal prism is shown) Type uniform polyhedron Faces 2+n total: 2 {n} n {4} Edges …   Wikipedia Dodecahedral cleavage — Cleavage Cleav age, n. 1. The act of cleaving or splitting. [1913 Webster] 2. (Crystallog.) The quality possessed by many crystallized substances of splitting readily in one or more definite directions, in which the cohesive attraction is a… …   The Collaborative International Dictionary of English List of mathematics articles (D) — NOTOC D D distribution D module D D Agostino s K squared test D Alembert Euler condition D Alembert operator D Alembert s formula D Alembert s paradox D Alembert s principle Dagger category Dagger compact category Dagger symmetric monoidal… …   Wikipedia Convex uniform honeycombs in hyperbolic space — The {5,3,4} honeycomb in 3D hyperbolic space, viewed in perspective In geometry, a convex uniform honeycomb is a tessellation of convex uniform polyhedron cells. In 3 dimensional hyperbolic space there are nine Coxeter group f …   Wikipedia Dodecahedron — Regular Dodecahedron (Click here for rotating model) Type Platonic solid Elements F = 12, E = 30 V = 20 (χ = 2) Faces by sides 12{5} …   Wikipedia Crystal habit — This article is about the descriptive term used in mineralogy. For the addictive drug, see crystal methamphetamine. Pyrite sun (or dollar) in laminated shale matrix. Between tightly spaced layers of shale, the aggregate was forced to grow in a… …   Wikipedia List of mathematics articles (O) — NOTOC O O minimal theory O Nan group O(n) Obelus Oberwolfach Prize Object of the mind Object theory Oblate spheroid Oblate spheroidal coordinates Oblique projection Oblique reflection Observability Observability Gramian Observable subgroup… …   Wikipedia Combination puzzle — Part of a series on Puzzles …   Wikipedia List of mathematics articles (T) — NOTOC T T duality T group T group (mathematics) T integration T norm T norm fuzzy logics T schema T square (fractal) T symmetry T table T theory T.C. Mits T1 space Table of bases Table of Clebsch Gordan coefficients Table of divisors Table of Lie …   Wikipedia Tesseract — For other uses, see Tesseract (disambiguation). Tesseract 8 cell 4 cube Schlegel diagram Type Convex regular 4 polytope …   Wikipedia 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”