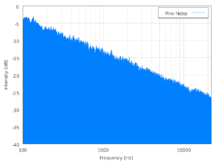
Pink noise

Pink noise
This article is about the signal in information theory. For the band, see PINKNOISE.
Colors of noise
White
Pink
Red (Brownian)
Grey

Pink noise or 1/ƒ noise (sometimes also called flicker noise) is a signal or process with a frequency spectrum such that the power spectral density (energy or power per Hz) is inversely proportional to the frequency. In pink noise, each octave carries an equal amount of noise power. The name arises from being intermediate between white noise (1/ƒ0) and red noise (1/ƒ2) which is commonly known as Brownian noise.

Within the scientific literature the term 1/ƒ noise is sometimes used a little more loosely to refer to any noise with a power spectral density of the form

S(f) \propto 1/f^\alpha

where ƒ is frequency and 0 < α < 2, with α usually close to 1. These "1/ƒ-like" noises occur widely in nature and are a source of considerable interest in many fields. The distinction between the noises with α near 1 and those with a broad range of α approximately corresponds to a much more basic distinction. The former (narrow sense) generally come from condensed matter systems in quasi-equilibrium, as discussed below.[1] The latter (broader sense) generally correspond to wide range of non-equilibrium driven dynamical systems.

The term flicker noise is sometimes used to refer to 1/ƒ noise, although this is more properly applied only to its occurrence in electronic devices due to a direct current. Mandelbrot and Van Ness proposed the name fractional noise (sometimes since called fractal noise) to emphasise that the exponent of the spectrum could take non-integer values and be closely related to fractional Brownian motion, but the term is very rarely used.

Contents

Description

Spectrum of a pink noise approximation. Power density falls off at 10 dB/decade.

There is equal energy in all octaves (or similar log bundles). In terms of power at a constant bandwidth, 1/ƒ noise falls off at 3 dB per octave. At high enough frequencies 1/ƒ noise is never dominant. (White noise is equal energy per hertz.)

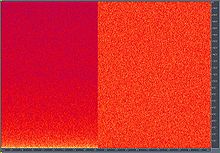Pink noise (left) and white noise (right) on an FFT spectrogram with linear frequency vertical axis (on a typical audio or similar spectrum analyzer the pink noise would be flat, not downward-sloping, and the white noise rising)

The human auditory system, which processes frequencies in a roughly logarithmic fashion approximated by the Bark scale, does not perceive them with equal sensitivity; signals in the 2–4-kHz octave sound loudest, and the loudness of other frequencies drops increasingly, depending both on the distance from the peak-sensitivity area and on the level. However, humans still differentiate between white noise and pink noise with ease.

Graphic equalizers also divide signals into bands logarithmically and report power by octaves; audio engineers put pink noise through a system to test whether it has a flat frequency response in the spectrum of interest. Systems that do not have a flat response can be equalized by creating a "mirror image" using a graphic equalizer. Because pink noise has a tendency to occur in natural physical systems it is often useful in audio production. Pink noise can be processed, filtered, and/or effects can be added to produce desired sounds. Pink noise generators are commercially available.

From a practical point of view, producing true pink noise is impossible, since the energy of such a signal would be infinite. That is, the energy of pink noise in any frequency interval from ƒ1 to ƒ2 is proportional to log(ƒ2/ƒ1), and if ƒ2 is infinity, so is the energy. Similarly, the energy of a pink noise signal would be infinite for ƒ1 = 0.

Practically, noise can be pink only over a specific range of frequencies. For ƒ2, there is an upper limit to the frequencies that can be measured.

One parameter of noise, the peak versus average energy contents, or crest factor, is important for testing purposes, such as for amplifier and loudspeaker capabilities. Various crest factors of pink noise can be used in simulations of various levels of dynamic range compression in music signals. A defined crest factor is also important for durability or heat tests on loudspeakers or power amplifiers, because the signal power is a direct function of the crest factor. On some digital pink noise generators the crest factor can be specified because the algorithm can be adjusted to never exceed certain levels.

Generalization to more than one dimension

The spectrum of pink noise is 1/f only for one-dimensional signals. For two-dimensional signals, e.g., images, the spectrum is reciprocal to f2. In general, in an n-dimensional system, the spectrum is reciprocal to fn. For higher-dimensional signals it is still true (by definition) that each octave carries an equal amount of noise power. The frequency spectrum of two-dimensional signals, for instance, is also two-dimensional, and the area covered by succeeding octaves is four times as large.

Occurrence

1/ƒ noise occurs in many physical, biological and economic systems. Some researchers describe it as being ubiquitous.[2] In physical systems it is present in some meteorological data series, the electromagnetic radiation output of some astronomical bodies, and in almost all electronic devices (referred to as flicker noise). In biological systems, it is present in heart beat rhythms, neural activity, and the statistics of DNA sequences. In financial systems it is often referred to as a long-term memory effect. Also, it describes the statistical structure of many natural images (images from the natural environment).[2] Recently, 1/f noise has also been successfully applied to the modeling of mental states in psychology.[3]

Richard F. Voss and J. Clarke claim that almost all musical melodies, when each successive note is plotted on a scale of pitches, will tend towards a pink noise spectrum.[4] Similarly, a generally 1/f distribution pattern has been observed in film shot length by researcher James E. Cutting of Cornell University, in the study of 150 popular movies released from 1935 to 2005.[5]

There are no simple mathematical models to create pink noise. It is usually generated by filtering white noise.[4][6][7]

There are many theories of the origin of 1/ƒ noise. Some theories attempt to be universal, while others are applicable to only a certain type of material, such as semiconductors. Universal theories of 1/ƒ noise remain a matter of current research interest.

Electronic devices

Main article: Flicker noise

A pioneering researcher in this field was Aldert van der Ziel.[citation needed]

In electronics, white noise will be stronger than pink noise (flicker noise) above some corner frequency. There is no known lower bound to pink noise in electronics. Measurements made down to 10−6 Hz (taking several weeks) have not shown a ceasing of pink-noise behaviour.[citation needed]

A pink noise source is sometimes included on analog synthesizers (although a white noise source is more common), both as a useful audio sound source for further processing, and also as a source of random control voltages for controlling other parts of the synthesizer.

The principal sources of 1/f noise in electronic devices are almost invariably the slow fluctuations of properties of the condensed-matter materials of the devices. In many cases the specific sources of the fluctuations are known. These include, inter alia, fluctuating configurations of defects in metals, fluctuating occupancies of traps in semiconductors, and fluctuating domain structures in magnetic materials.[1] [8] The explanation for the approximately 1/f spectral form turns out to be relatively trivial, usually coming from a distribution of kinetic activation energies of the fluctuating processes.[9] Since the frequency range of the typical noise experiment (e.g. 1 Hz–1 kHz) is low compared with typical microscopic "attempt frequencies" (e.g. 1014 Hz), the exponential factors in the Arrhenius equation for the rates are large. Relatively small spreads in the activation energies appearing in these exponents then result in large spreads of characteristic rates. In the simplest toy case, a flat distribution of activation energies gives exactly a 1/f spectrum, because d(ln(f))/df = 1/f.

See also

References

Footnotes

  1. ^ a b Kogan, Shulim (1996). Electronic Noise and Fluctuations in Solids. [Cambridge University Press]. ISBN 0521460344. 
  2. ^ a b Bak, P. and Tang, C. and Wiesenfeld, K. (1987). "Self-Organized Criticality: An Explanation of 1/ƒ Noise". Physical Review Letters 59 (4): 381–384. Bibcode 1987PhRvL..59..381B. doi:10.1103/PhysRevLett.59.381. 
  3. ^ Van Orden, G.C. and Holden, J.G. and Turvey, M.T. (2003). "Self-organization of cognitive performance". Journal of Experimental Psychology: general 132 (3): 331–350. doi:10.1037/0096-3445.132.3.331. 
  4. ^ a b Noise in Man-generated Images and Sound
  5. ^ Anger, Natalie (March 1, 2010). "Bringing New Understanding to the Director's Cut". The New York Times. Retrieved on March 3, 2010. See also original study
  6. ^ DSP Generation of Pink Noise
  7. ^ http://linkage.rockefeller.edu/wli/moved.8.04/1fnoise/mcclain01.pdf
  8. ^ Weissman, M. B. (1988). "1/ƒ Noise and other slow non-exponential kinetics in condensed matter". Reviews of Modern Physics 60 (2): 537–571. Bibcode 1988RvMP...60..537W. doi:10.1103/RevModPhys.60.537. 
  9. ^ Dutta, P. and Horn, P. M. (1981). "Low-frequency fluctuations in solids: 1/ƒ noise". Reviews of Modern Physics 53 (3): 497–516. Bibcode 1981RvMP...53..497D. doi:10.1103/RevModPhys.53.497. 

Notations

  • Kogan, Shulim (1996). Electronic Noise and Fluctuations in Solids. [Cambridge University Press]. ISBN 0521460344. 

External links


Wikimedia Foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Look at other dictionaries:

  • Pink Noise — Das 1/f Rauschen (auch „Rosa Rauschen“ genannt) bezeichnet ein Rauschen, das mit steigender Frequenz abnimmt. Die Amplitude kann als normalverteilt angesehen werden, der Frequenzgang verläuft umgekehrt proportional zur Frequenz ( 1/f) und die… …   Deutsch Wikipedia

  • pink noise — a random signal within the audible frequency range whose amplitude decreases as frequency increases, maintaining constant audio power per frequency increment. [1960 65] * * * pink noise noun Noise of mid to low frequency • • • Main Entry: ↑pink * …   Useful english dictionary

  • pink noise — noun A signal or process with a frequency spectrum such that the spectral energy density is proportional to the reciprocal of the frequency. It was Gilden, Thorton, and Mallon (1995) who first reported pink noise in response time variability… …   Wiktionary

  • pink noise — noun Physics random noise having equal energy per octave, and so having more low frequency components than white noise …   English new terms dictionary

  • pink noise — /pɪŋk ˈnɔɪz/ (say pingk noyz) noun an electronically produced noise used for experimental purposes as sound machinery, etc., in which all frequencies are represented with equal energy in each octave, that is with as much energy between 100 Hz and …  

  • pink noise — noun Date: 1961 a mixture of sound waves with an intensity that diminishes proportionally with frequency to yield approximately equal energy per octave compare white noise …   New Collegiate Dictionary

  • pink noise — a random signal within the audible frequency range whose amplitude decreases as frequency increases, maintaining constant audio power per frequency increment. [1960 65] * * * …   Universalium

  • pink noise — F/A/V a sound that has equal energy (constant power) in each 1/3 octave band …   Audio and video glossary

  • Pink noise — F/A/V A sound signal that has an equal amount of energy per octave or fraction of an octave. (Sound) …   Audio and video glossary

  • Noise (audio) — Noise in audio, recording, and broadcast systems refers to the residual low level sound (usually hiss and hum) that is heard in quiet periods of a programme. In audio engineering, it can refer either to the acoustic noise from loudspeakers, or to …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”