Curved mirror

Reflections in a spherical convex mirror. The photographer is seen reflected at top right

A curved mirror is a mirror with a curved reflective surface, which may be either convex (bulging outward) or concave (bulging inward). Most curved mirrors have surfaces that are shaped like part of a sphere, but other shapes are sometimes used in optical devices. The most common non-spherical type are parabolic reflectors, found in optical devices such as reflecting telescopes that need to image distant objects, since spherical mirror systems suffer from spherical aberration.

Convex mirrors

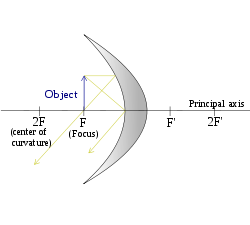
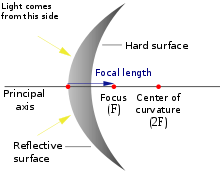A convex mirror diagram showing the focus, focal length, centre of curvature, principal axis, etc

A convex mirror, fish eye mirror or diverging mirror, is a curved mirror in which the reflective surface bulges toward the light source. Convex mirrors reflect light outwards, therefore they are not used to focus light. Such mirrors always form a virtual image, since the focus (F) and the centre of curvature (2F) are both imaginary points "inside" the mirror, which cannot be reached. As a result, images formed by these mirrors cannot be projected on a screen, since the image is inside the mirror.

A collimated (parallel) beam of light diverges (spreads out) after reflection from a convex mirror, since the normal to the surface differs with each spot on the mirror.

Uses

Convex mirror lets motorists see around a corner.

Detail of the convex mirror in the Arnolfini Portrait

The passenger-side mirror on a car is typically a convex mirror. In some countries, these are labeled with the safety warning "Objects in mirror are closer than they appear", to warn the driver of the convex mirror's distorting effects on distance perception. Convex mirrors are preferred in vehicles because they give an upright, though diminished, image. Also they provide a wider field of view as they are curved outwards.

Convex mirrors are used in some automated teller machines as a simple and handy security feature, allowing the users to see what is happening behind them. Similar devices are sold to be attached to ordinary computer monitors.

Some camera phones use convex mirrors to allow the user to correctly aim the camera while taking a self-portrait.

Round convex mirrors called Oeil de Sorcière (French for "sorcerer's eye") were a popular luxury item from the 15th century onwards, shown in many depictions of interiors from that time.^[1] With 15th century technology, it was easier to make a regular curved mirror (from blown glass) than a perfectly flat one. They were also known as "bankers' eyes" due to the fact that their wide field of vision was useful for security. Famous examples in art include the Arnolfini Portrait by Jan van Eyck and the left wing of the Werl Altarpiece by Robert Campin.^[2]

Image

The image on a convex mirror is always virtual (rays haven't actually passed through the image, their extensions do, like in a regular mirror), diminished (smaller), and upright. As the object gets closer to the mirror, the image gets larger, until reaching approximately the size of the object, when it touches the mirror. As the object moves away, the image diminishes in size and gets gradually closer to the focus, until it is reduced to a point in the focus when the object is at an infinite distance. These features make convex mirrors very useful: since everything appears smaller in the mirror, they cover a wider field of view than a normal plane mirror does.

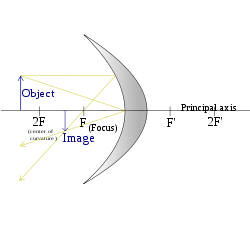
Effect on image of object's position relative to mirror focal point (convex)

Object's position (S), focal point (F)	Image	Diagram
$S>F,\ S=F,\ S<F$	Virtual Upright Reduced (diminished/smaller)

Concave mirrors

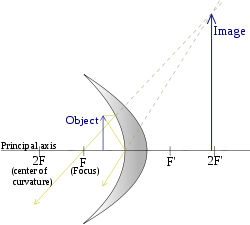
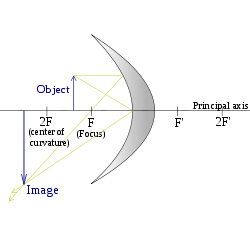
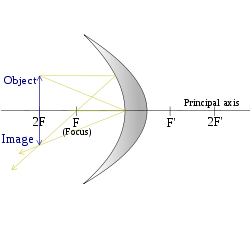
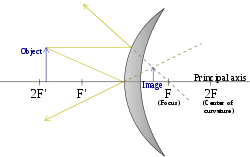
A concave mirror diagram showing the focus, focal length, centre of curvature, principal axis, etc.

A concave mirror, or converging mirror, has a reflecting surface that bulges inward (away from the incident light). Concave mirrors reflect light inward to one focal point.They are used to focus light. Unlike convex mirrors, concave mirrors show different image types depending on the distance between the object and the mirror.

These mirrors are called "converging" because they tend to collect light that falls on them, refocusing parallel incoming rays toward a focus. This is because the light is reflected at different angles, since the normal to the surface differs with each spot on the mirror.

Uses

See also: optical cavity and laser construction

Image

Effect on image of object's position relative to mirror focal point (concave)

Object's position (S), focal point (F)	Image	Diagram
S < F (Object between focal point and mirror)	Virtual Upright Magnified (larger)
S = F (Object at focal point)	Reflected rays are parallel and never meet, so no image is formed. In the limit where S approaches F, the image distance approaches infinity, and the image can be either real or virtual and either upright or inverted depending on whether S approaches F from above or below.
F < S < 2F (Object between focus and centre of curvature)	Real Inverted (vertically) Magnified (larger)
S = 2F (Object at centre of curvature)	Real Inverted (vertically) Same size Image formed at centre of curvature
S > 2F (Object beyond centre of curvature)	Real Inverted (vertically) Reduced (diminished/smaller) As the distance of the object increases, the image asymptotically approaches the focal point In the limit where S approaches infinity, the image size approaches zero as the image approaches F

Mirror shape

Most curved mirrors have a spherical profile. These are the simplest to make, and it is the best shape for general-purpose use. Spherical mirrors, however, suffer from spherical aberration. Parallel rays reflected from such mirrors do not focus to a single point. For parallel rays, such as those coming from a very distant object, a parabolic reflector can do a better job. Such a mirror can focus incoming parallel rays to a much smaller spot than a spherical mirror can.

See also: Toroidal reflector

Analysis

Mirror equation and magnification

The Gaussian mirror equation relates the object distance d_o and image distance d_i to the focal length f:^[3]

$\frac{1}{d_\mathrm{o}}+ \frac{1}{d_\mathrm{i}} = \frac{1}{f}$.

The sign convention used here is that the focal length is positive for concave mirrors and negative for convex ones, and d_o and d_i are positive when the object and image are in front of the mirror, respectively. (They are positive when the object or image is real.)^[3]

For convex mirrors, if one moves the 1 / d_o term to the right side of the equation to solve for 1 / d_i, the result is always a negative number, meaning that the image distance is negative—the image is virtual, located "behind" the mirror. This is consistent with the behavior described above.

For concave mirrors, whether the image is virtual or real depends on how large the object distance is compared to the focal length. If the 1 / f term is larger than the 1 / d_o term, 1 / d_i is positive and the image is real. Otherwise, the term is negative and the image is virtual. Again, this validates the behavior described above.

The magnification of a mirror is defined as the height of the image divided by the height of the object:

$m \equiv \frac{h_\mathrm{i}}{h_\mathrm{o}} = - \frac{d_\mathrm{i}}{d_\mathrm{o}}$.

By convention, if the resulting magnification is positive, the image is upright. If the magnification is negative, the image is inverted (upside down).

Ray tracing

Main article: Ray tracing (physics)

The image location and size can also be found by graphical ray tracing, as illustrated in the figures above. A ray drawn from the top of the object to the surface vertex (where the optical axis meets the mirror) will form an angle with that axis. The reflected ray has the same angle to the axis, but is below it (See Specular reflection).

A second ray can be drawn from the top of the object passing through the focal point and reflecting off the mirror at a point somewhere below the optical axis. Such a ray will be reflected from the mirror as a ray parallel to the optical axis. The point at which the two rays described above meet is the image point corresponding to the top of the object. Its distance from the axis defines the height of the image, and its location along the axis is the image location. The mirror equation and magnification equation can be derived geometrically by considering these two rays.

Ray transfer matrix of spherical mirrors

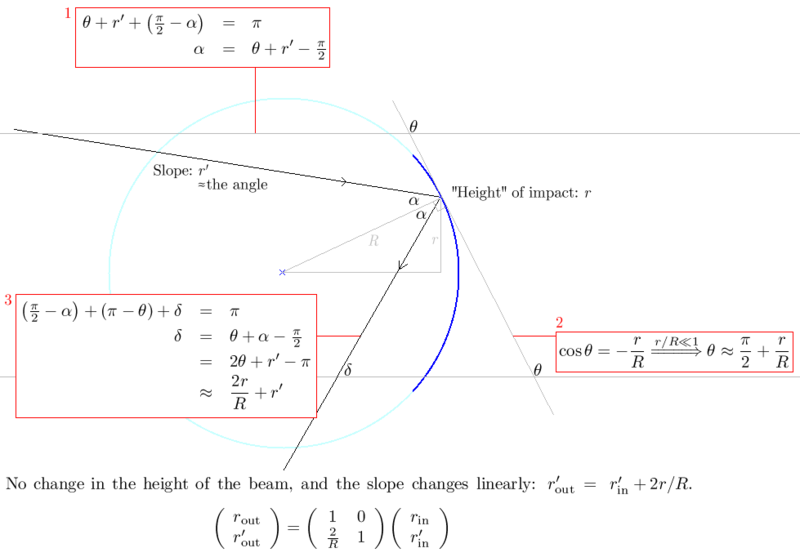
Further information: Ray transfer matrix analysis

The mathematical treatment is done under the paraxial approximation, meaning that under the first approximation a spherical mirror is a parabolic reflector. The ray matrix of a spherical mirror is shown here for the concave reflecting surface of a spherical mirror. The C element of the matrix is $-\frac{1}{f}$, where f is the focal point of the optical device.

Boxes 1 and 3 feature summing the angles of a triangle and comparing to π radians (or 180°). Box 2 shows the Maclaurin series of $\arccos\left(-\frac{r}{R}\right)$ up to order 1. The derivations of the ray matrices of a convex spherical mirror and a thin lens are very similar.

See also

• List of telescope parts and construction
• Lens (optics)

References

1. ^ Venice Botteghe: Antiques, Bijouterie, Coffee, Cakes, Carpet, Glass
2. ^ Lorne Campbell, National Gallery Catalogues (new series): The Fifteenth Century Netherlandish Paintings, pp. 178-179, 188-189, 1998, ISBN 185709171X
3. ^ ^{a b} Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. p. 160–1. ISBN 0-201-11609-X. 

External links

• [1] Java Applet to explore ray tracing.
• [2] Java applets to explore ray tracing for curved mirrors.
• Concave mirrors — real images Molecular Expressions Optical Microscopy Primer.
• Spherical mirrors Online physics lab.
• "Grinding the World's Largest Mirror" Popular Science, December 1935