- Equals sign
-
Due to technical restrictions, ":=" redirects here. For the computer programming assignment operator, see Assignment (computer programming). For the definition symbol, see List of mathematical symbols#Symbols."=" and "=" redirect here. For double hyphens, see Double hyphen.For other uses, see Equals (disambiguation).
 A well-known equality featuring the equals sign, often used in the phrases, "put two and two together," and, "As easy as two plus two."
A well-known equality featuring the equals sign, often used in the phrases, "put two and two together," and, "As easy as two plus two."
The equality sign, equals sign, or "=" is a mathematical symbol used to indicate equality. It was invented in 1557 by Robert Recorde. The equals sign is placed between the things stated to have the same value, as in an equation. It is the Unicode and ASCII character 003D (in hexadecimal).
Contents
History
The etymology of the word equal is from the Latin word aequalis, meaning "uniform, identical, or equal," from aequus "level, even, just."
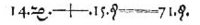 The first use of an equals sign, equivalent to 14x+15=71 in modern notation. From The Whetstone of Witte by Robert Recorde.
The first use of an equals sign, equivalent to 14x+15=71 in modern notation. From The Whetstone of Witte by Robert Recorde.
The "=" symbol that is now universally accepted by mathematics for equality was first recorded by Welsh mathematician Robert Recorde in The Whetstone of Witte (1557). The original form of the symbol was much wider than the present form. In his book Recorde explains his design of the "Gemowe lines" (meaning twin lines, from the Latin gemini):
...to auoide the tediouſe repetition of theſe woordes : is equalle to : I will ſette as I doe often in woorke vſe, a paire of paralleles, or Gemowe lines of one lengthe, thus: =, bicauſe noe .2. thynges, can be moare equalle.
...to avoid the tedious repetition of these words: "is equal to", I will set (as I do often in work use) a pair of parallels (or Gemowe[1] lines) of one length (thus =), because no two things can be more equal.
According to Scotland's St Andrews University Maths History website:[2]
The symbol '=' was not immediately popular. The symbol || was used by some and æ (or œ), from the Latin word aequalis meaning equal, was widely used into the 1700s.
Usage
In mathematics, the equals sign is used for definitions (ex: let x = 2) as well as conditions and denoted equalities (ex: if x = 2 then x/2 = 1).
The equals sign is also used as a grammatical tone letter in the orthographies of Budu in the Congo-Kinshasa, in Krumen, Mwan and Dan in the Ivory Coast.[3][4] The Unicode character used for the tone letter (U+A78A)[5] is different from the mathematical symbol (U+003D).
In computer programming
Traditional computer programming languages and their descendants (e.g. the Algol family, Pascal family, ADA, Eiffel, etc) use the equals sign as a boolean equality-operator as well as for defining constants, types, and parameters. This is consistent with mathematical usage and marks an intention for such languages to be as similar as possible to mathematical notation. A colon-equals (
:=) is typically used to denote assignment.In C-like languages, it is instead used as an assignment operator. C-like languages therefore use a double equals sign (
==) as an equality operator.Some languages (e.g. BASIC) use a single equals sign to denote both functions, sometimes with an optional
letkeyword to resolve any ambiguities.Usage of several equal-signs
In PHP, the triple equals sign (
===) denotes identicalness,[6] meaning that not only do the two values evaluate to the same boolean value, they are also of the same data type. For instance, the expression0 == falseis true, but0 === falseis not, because the number 0 is an integer value (whereas false is a boolean).JavaScript has the same semantics for
===, referred to as "equality without type coercion". However in JavaScript the behavior of==cannot be described by any simple consistent rules. The expression0 == falseis true, but0 == undefinedis false, even though both sides of the==act the same in boolean context. For this reason it is recommended to avoid the==operator in JavaScript in favor of===.[7]In Ruby, equality under
==requires both operands to be of identical type, e.g.0 == falseis false. The===operator is flexible and may be defined arbitrarily by any given type. For example a value of typeRangeis a range of integers, such as1800..1899.(1800..1899) == 1844is false, since the types are different (Range vs. Integer); however(1800..1899) === 1844is true, since Range defines===to mean "inclusion in the range".[8] Note that under these semantics,===is non-commutative; e.g.1844 === (1800..1899)is false, since it is interpreted to meanInteger#===rather thanRange#===.[9]Related symbols
See also: Unicode mathematical operatorsApproximately equal
Symbols used to denote items that are approximately equal are "wavy" equals signs.
- ≈ (Unicode 2248),
- ≃ (Unicode 2243), a combination of ≈ and =, also used to indicate asymptotically equal to
- ≅ (Unicode 2245), another combination of ≈ and =, which is also sometimes used to indicate isomorphism or congruence
- ~ (Unicode 007E), which is also sometimes used to indicate proportionality
- ≒ (Unicode 2252), in Japanese, this is commonly used.
Not equal
The symbol used to denote inequation — when items are not equal — is a slashed equals sign "≠" (Unicode 2260).
Most programming languages, limiting themselves to the ASCII character set, use
~=,!=,/=,=/=, or<>to represent their boolean inequality operator.Identity
The triple bar symbol "≡" (U+2261) is often used to indicate an identity, a definition (which can also be represented by "≝", U+225D), or a congruence relation in modular arithmetic. The symbol "≘" can be used to express that an item corresponds to another.
Isomorphism
The symbol "≅" is often used to indicate isomorphic algebraic structures or congruent geometric figures.
In logic
Equality of truth values, i.e. bi-implication or logical equivalence, may be denoted by various symbols including =, ~, and ⇔.
In a double-barreled name
A possibly unique case of the equal sign in a person's name, specifically in a double-barreled name, was by pioneer aviator Alberto Santos=Dumont, as he is also known to not only have often used an equal sign (=) between his two surnames in place of a hyphen, but also seems to have personally preferred that practice, to display equal respect for his father's French ethnicity and the Brazilian ethnicity of his mother.[10]
Misconceptions
The equals sign can be used incorrectly within a mathematical argument, if used in a manner that connects steps of math in a non-standard way, rather than to show equality. For example, if one were finding the sum of the numbers 1, 2, 3, 4, and 5, one might say: 1 + 2 = 3 + 3 = 6 + 4 = 10 + 5 = 15. This is clearly incorrect, because each part of the equality has a different value. If interpreted strictly as it says, it implies 3 = 6 = 10 = 15 = 15. A correct version of the argument would be 1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15[11].
See also
Notes
- ^ From Latin gamellus, twin.
- ^ The MacTutor History of Mathematics archive
- ^ Peter G. Constable, Lorna A. Priest, Proposal to Encode Additional Orthographic and Modifier Characters, 2006.
- ^ Hartell, Rhonda L., ed. (1993), The Alphabets of Africa. Dakar: UNESCO and SIL.
- ^ Unicode Latin Extended-D code chart http://www.unicode.org/charts/PDF/UA720.pdf
- ^ http://www.php.net/manual/en/language.operators.comparison.php
- ^ Doug Crockford, "JavaScript: The Good Parts". http://tumblr.iamdanw.com/post/107829021/fasturtle-doug-crockford-says-to-never-use-the
- ^ Why's (Poignant) Guide to Ruby, Chapter 5 Section 1, "This One's for the Disenfranchised" http://mislav.uniqpath.com/poignant-guide/book/chapter-5.html#section1
- ^ Brett Rasmussen, "Don't Call it Case Equality" http://www.pmamediagroup.com/2009/07/dont-call-it-case-equality/
- ^ Gray, Carroll F. (November 2006). "The 1906 Santos=Dumont No. 14bis". World War I Aeroplanes No. 194: 4.
- ^ http://tamu.academia.edu/SencerCorlu/Papers/522225/Capraro_R._M._Capraro_M._M._Yetkiner_Z._E._Corlu_M._S._Ozel_S._Ye_S._and_Kim_H._G._2011_._An_international_perspective_between_problem_types_in_textbooks_and_students_understanding_of_relational_equality._Mediterranean_Journal_for_Research_in_Mathematics_Education_An_International_Journal_10_187-213
References
- Cajori, Florian (1993). A History of Mathematical Notations. New York: Dover (reprint). ISBN 0-486-67766-4.
- Boyer, C. B.: A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7)
External links
Categories:- Mathematical symbols
Wikimedia Foundation. 2010.

