Logical equality

For the corresponding concept in combinational logic, see XNOR gate.

XNOR Logic Gate Symbol

Logical equality is a logical operator that corresponds to equality in Boolean algebra and to the logical biconditional in propositional calculus. It gives the functional value true if both functional arguments have the same logical value, and false if they are different.

It is customary practice in various applications, if not always technically precise, to indicate the operation of logical equality on the logical operands x and y by any of the following forms:

$\begin{matrix} x \leftrightarrow y & \quad & \quad & x \Leftrightarrow y & \quad & Exy \\ x \ \mbox{EQ} \ y & \quad & \quad & x = y \end{matrix}$

Some logicians, however, draw a firm distinction between a functional form, like those in the lefthand column, which they interpret as an application of a function to a pair of arguments — and thus a mere indication that the value of the compound expression depends on the values of the component expressions — and an equational form, like those in the righthand column, which they interpret as an assertion that the arguments have equal values, in other words, that the functional value of the compound expression is true.

In mathematics, the plus sign "+" almost invariably indicates an operation that satisfies the axioms assigned to addition in the type of algebraic structure that is known as a field. For boolean algebra, this means that the logical operation signified by "+" is not the same as the inclusive disjunction signified by "∨" but is actually equivalent to the logical inequality operator signified by "≠", or what amounts to the same thing, the exclusive disjunction signified by "XOR". Naturally, these variations in usage have caused some failures to communicate between mathematicians and switching engineers over the years. At any rate, one has the following array of corresponding forms for the symbols associated with logical inequality:

$\begin{matrix} x + y & \quad & \quad & x \not\equiv y & \quad & Jxy \\ x \ \mbox{XOR} \ y & \quad & \quad & x \ne y \end{matrix}$

This explains why "EQ" is often called "XNOR" in the combinational logic of circuit engineers, since it is the Negation of the XOR operation; NXOR is a less commonly used alternative.[1] Another rationalization of the admittedly circuitous name "XNOR" is that one begins with the "both false" operator NOR and then adds the eXception, "or both true".

Definition

Logical equality is an operation on two logical values, typically the values of two propositions, that produces a value of true if and only if both operands are false or both operands are true.

The truth table of p EQ q (also written as p = q, p ↔ q, or p ≡ q, or p == q) is as follows:

Logical Equality

p	q	p = q
0	0	1
0	1	0
1	0	0
1	1	1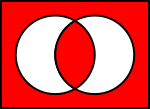

The Venn diagram of A EQ B (red part is true)

Alternative descriptions

The form (x = y) is equivalent to the form (x ∧ y) ∨ (¬x ∧ ¬y).

$(x = y) = \lnot(x \oplus y) = (x \land y) \lor (\lnot x \land \lnot y) = (\lnot x \lor y) \land (x \lor \lnot y)$

For the operands x and y, the truth table of the logical equality operator is as follows:

$x \leftrightarrow y$		y
		T	F
x	T	T	F
	F	F	T

See also

Thinking portal

Ampheck Boolean function If and only if

Logical equivalence Logical biconditional Propositional calculus

External links

• Mathworld, XNOR