- Morera's theorem
-
In complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic.
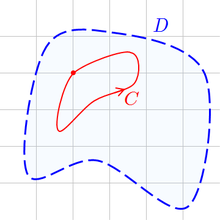
Morera's theorem states that a continuous, complex-valued function ƒ defined on a connected open set D in the complex plane that satisfies
for every closed piecewise C1 curve γ in D must be holomorphic on D.
The assumption of Morera's theorem is equivalent to that ƒ has an anti-derivative on D.
The converse of the theorem is not true in general. A holomorphic function need not possess an antiderivative on its domain, unless one imposes additional assumptions. The converse does hold e.g. if the domain is simply connected; this is Cauchy's integral theorem, stating that the line integral of a holomorphic function along a closed curve is zero.
Contents
Proof
There is a relatively elementary proof of the theorem. One constructs an anti-derivative for ƒ explicitly. The theorem then follows from the fact that holomorphic functions are analytic.
Without loss of generality, it can be assumed that D is connected. Fix a point z0 in D, and for any
 , let
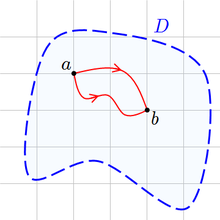
, let ![\gamma: [0,1]\to D](7/eb79a64501a53683b50a69996a7c462f.png) be a piecewise C1 curve such that γ(0) = z0 and γ(1) = z. Then define the function F to be
be a piecewise C1 curve such that γ(0) = z0 and γ(1) = z. Then define the function F to beTo see that the function is well-defined, suppose
![\tau: [0,1]\to D](9/0b9c63f04978f88609efd8e49b0e8fdc.png) is another piecewise C1 curve such that τ(0) = z0 and τ(1) = z. The curve γτ − 1 (i.e. the curve combining γ with τ in reverse) is a closed piecewise C1 curve in D. Then,
is another piecewise C1 curve such that τ(0) = z0 and τ(1) = z. The curve γτ − 1 (i.e. the curve combining γ with τ in reverse) is a closed piecewise C1 curve in D. Then,And it follows that
By continuity of f and the definition of the derivative, we get that F'(z) = f(z). Note that we can apply neither the Fundamental theorem of Calculus nor the mean value theorem since they are only true for real-valued functions.
Since f is the derivative of the holomorphic function F, it is holomorphic. This completes the proof.
Applications
Morera's theorem is a standard tool in complex analysis. It is used in almost any argument that involves a non-algebraic construction of a holomorphic function.
Uniform limits
For example, suppose that ƒ1, ƒ2, ... is a sequence of holomorphic functions, converging uniformly to a continuous function ƒ on an open disc. By Cauchy's theorem, we know that
for every n, along any closed curve C in the disc. Then the uniform convergence implies that
for every closed curve C, and therefore by Morera's theorem ƒ must be holomorphic. This fact can be used to show that, for any open set Ω ⊆ C, the set A(Ω) of all bounded, analytic functions u : Ω → C is a Banach space with respect to the supremum norm.
Infinite sums and integrals
Morera's theorem can also be used in conjunction with Fubini's theorem to show the analyticity of functions defined by sums or integrals, such as the Riemann zeta function
or the Gamma function
Specifically one shows that
for a suitable closed curve C, by writing
and then using Fubini's theorem to justify changing the order of integration, getting
Then one uses the analyticity of x ↦ xα−1 to conclude that
and hence the double integral above is 0. Similarly, in the case of the zeta function, Fubini's theorem justifies interchanging the integral along the closed curve and the sum.
Weakening of hypotheses
The hypotheses of Morera's theorem can be weakened considerably. In particular, it suffices for the integral
to be zero for every closed triangle T contained in the region D. This in fact characterizes holomorphy, i.e. ƒ is holomorphic on D if and only if the above conditions hold.
See also
- Cauchy–Riemann equations
- Methods of contour integration
- Residue (complex analysis)
References
- Ahlfors, Lars (January 1, 1979), Complex Analysis, International Series in Pure and Applied Mathematics, McGraw-Hill, ISBN 978-0070006577, Zbl 0395.30001.
- Conway, John B. (1973), Functions of One Complex Variable I, Graduate Texts in Mathematics, 11, Springer Verlag, ISBN 978-3540903284, Zbl 0277.30001.
- Greene, Robert E.; Krantz, Steven G. (2006), Function Theory of One Complex Variable, Graduate Studies in Mathematics, 40, American Mathematical Society, ISBN 0-8218-3962-4
- Morera, Giacinto (1886), "Un teorema fondamentale nella teorica delle funzioni di una variabile complessa", Rendiconti del Reale Instituto Lombardo di Scienze e Lettere 19 (2): 304–307, JFM 18.0338.02, archived from the original on unspecified date, http://www.archive.org/stream/rendiconti00unkngoog#page/n312/mode/2up (in Italian).
- Rudin, Walter (1987) [1966], Real and Complex Analysis (3rd ed.), McGraw-Hill, pp. xiv+416, ISBN 978-0070542341, Zbl 0925.00005.
External links
Categories:- Complex analysis
- Theorems in complex analysis
Wikimedia Foundation. 2010.