- Stellated octahedron
-
Stellated octahedron 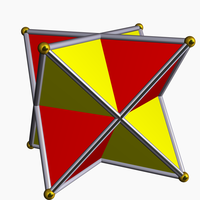
Type Regular compound Coxeter-Dynkin diagram 

 +
+ 


Schläfli symbol {{3,3}} Stellation core Octahedron Convex hull Cube Index UC4, W19 Polyhedra 2 tetrahedra Faces 8 triangles Edges 12 Vertices 8 Dual Self-dual Symmetry group octahedral (Oh), [4,3] or [[3,3]] Subgroup restricting to one constituent tetrahedral (Td)
[3,3]The stellated octahedron, or stella octangula, is the only stellation of the octahedron. It was named by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in Pacioli's Divina Proportione, 1509.
It is the simplest of five regular polyhedral compounds.
It can be seen as either a polyhedron compound or a stellation:
As a compound, it is constructed as the union of two tetrahedra (a tetrahedron and its dual tetrahedron). The vertex arrangement of the two tetrahedra is shared by a cube. The intersection of the two tetrahedra form an inner octahedron, which shares the same face-planes as the compound.
It can be seen as an octahedron with tetrahedral pyramids on each face. It has the same topology as the convex Catalan solid, the triakis octahedron, which has much shorter pyramids.
The stellation facets are very simple:
 (See Wenninger model W19.)
(See Wenninger model W19.)It can also be constructed from eight of the 20 vertices of the dodecahedron.
Contents
Artistic references
The Stellated octahedron and other polyhedra appear in M. C. Escher's print "Stars".
Gallery

It is the only fully symmetric facetting of the cube






This polyhedron-related article is a stub. You can help Wikipedia by expanding it.
