Measurement of a Circle

Measurement of a Circle (Greek: Κύκλου μέτρησις, Kuklou metrēsis) is a treatise that consists of three propositions by Archimedes. The treatise is only a fraction of what was a longer work.^[1][2]

Propositions

Proposition one

The circle and the triangle are equal in area.

Proposition one states:

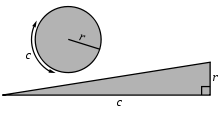
The area of any circle is equal to a right-angled triangle in which one of the sides about the right angle is equal to the radius, and the other to the circumference, of the circle.

Any circle with a circumference c and a radius r is equal in area with a right triangle with the two legs being c and r. This proposition is proved by the method of exhaustion.^[3]

Proposition two

Proposition two states:

The area of a circle is to the square on its diameter as 11 to 14.

This proposition could not have been placed by Archimedes, for it relies on the outcome of the third proposition.^[3]

Proposition three

Examples of how Archimedes calculated pi. Archimedes used a 96-sided polygon to find his estimate.

Proposition three states:

The ratio of the circumference of any circle to its diameter is greater than $3\tfrac{10}{71}$ but less than $3\tfrac{1}{7}$.

This approximates what we now call the mathematical constant π. He found these bounds on the value of π by inscribing and circumscribing a circle with two similar 96-sided regular polygons.^[4]

Approximation to square roots

This proposition also contains accurate approximations to the square root of 3 (one larger and one smaller) and other larger non-perfect square roots; however, Archimedes gives no explanation as to how he found these numbers.^[2] He gives the upper and lower bounds to √3 as  $\tfrac{1351}{780} > \sqrt{3} > \tfrac{265}{153}\,.$^[3] However, these bounds are familiar from the study of Pell's equation and the convergents of an associated continued fraction, leading to much speculation as to how much of this number theory might have been accessible to Archimedes. Discussion of this approach goes back at least to Thomas Fantet de Lagny, FRS (compare Chronology of computation of π) in 1723, but was treated more explicitly by Hieronymus Georg Zeuthen. In the early 1880s, Friedrich Otto Hultsch (1833--1906) and Karl Heinrich Hunrath (b. 1847) noted how the bounds could be found quickly by means of simple binomial bounds on square roots close to a perfect square modelled on Elements II.4, 7; this method is favoured by Heath. Although only one route to the bounds is mentioned, in fact there are two others, making the bounds almost inescapable however the method is worked. But the bounds can also be produced by an iterative geometrical construction suggested by Archimedes' Stomachion in the setting of the regular dodecagon. In this case, the task is to give rational approximations to the tangent of π/12.

References

1. ^ Heath, Thomas Little (1921), A History of Greek Mathematics, Boston: Adamant Media Corporation, ISBN 0543968774, http://books.google.com/?id=zGIYbEtzD-QC&printsec=frontcover, retrieved 2008-06-30 
2. ^ ^{a b} "Archimedes". Encyclopædia Britannica. 2008. http://www.britannica.com/EBchecked/topic/32808/Archimedes. Retrieved 2008-06-30. 
3. ^ ^{a b c} Heath, Thomas Little (1897), The Works of Archimedes, Cambridge University, pp. lxxvii ; 50, http://www.archive.org/details/worksofarchimede029517mbp, retrieved 2008-06-30 
4. ^ Heath, Thomas Little (1931), A Manual of Greek Mathematics, Mineola, N.Y.: Dover Publications, p. 146, ISBN 0486432319, http://books.google.com/?id=_HZNr_mGFzQC&printsec=frontcover