Rail adhesion

Driving wheel of steam locomotive

The term adhesion railway or adhesion traction describes the most common type of railway, where power is applied by driving some or all of the wheels of the locomotive. Thus, it relies on the friction between a steel wheel and a steel rail. Note that steam locomotives of old were driven only by 'drivers' that were connected to the 'side rods' of the locomotive. These were the large wheels. On diesels, traction electric motors (DC or AC) drive all or some of the axles. Both steam locomotives of old and many modern diesels have sand tubes that deposit quantities of dried sand directly to the rail heads directly in front of most/all axles. When an engine slips, particularly when starting a heavy train, sand applied at the front of the driving wheels greatly aids in tractive effort causing the train to 'lift', or to commence the motion intended by the engine driver.

The term is particularly used when discussing conventional railways to distinguish from other forms of traction such as funicular or cog railway For example, the Bernese Oberland Railway "is a mixed rack and adhesion railway".^[1]

Traction or friction can be reduced when the rails are greasy, because of rain, oil or decomposing leaves which compact into a hard slippery lignin coating. On an adhesion railway, most locomotives will have a sand containment vessel. Properly dried sand can be dropped on to the rail to improve traction under slippery conditions. The sand is most often applied using compressed air.

Measures against reduced adhesion due to leaves include application of 'Sandite' (a gel-sand mix) by special sanding trains, scrubbers and water jets, and long-term management of railside vegetation.

Effect of adhesion limits

See also: Traction (engineering)

Adhesion is caused by friction, with maximum tangential force produced by a driving wheel before slipping given by:

F_max= coefficient of friction x Weight on wheel

Usually the force needed to start sliding is greater than that needed to continue sliding. The former is concerned with static friction, referred colloquially to as 'stiction', or 'limiting friction', whilst the latter is called 'sliding friction'.

For steel on steel, the coefficient of friction can be as high as 0.78, under the best of conditions (= utopic laboratory condition, on railway realty: 0.35 -0.5 ^[2]), whilst under extreme conditions it can fall to as low as 0.05. Thus a 100 tonne locomotive could have a tractive effort of 350 kilonewton, under the ideal conditions (assuming sufficient force can be produced by the engine), falling to a 50 kilonewton under the worst conditions.

All-weather adhesion

This term (all weather adhesion) is usually used in American continent and refers to the adhesion available during traction mode with 99% reliability in all weather conditions.

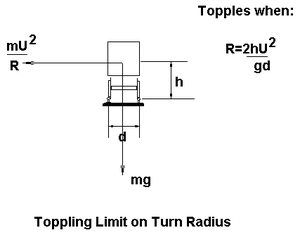
Toppling conditions

The maximum speed a train can proceed around a turn is limited by the radius of turn, the position of the centre of mass of the units, the wheel gauge and whether the track is superelevated or canted (see cant (road/rail)).

Toppling will occur when the overturning moment due to the side force (centrifugal acceleration) is sufficient to cause the inner wheel to begin to lift off the rail. This may result in loss of adhesion - causing the train to slow, preventing toppling. Alternatively, the inertia may be sufficient to cause the train to continue to move at speed causing the vehicle to topple completely.

For a wheel gauge of 1.5 m, no canting, a centre of gravity height of 3 m and speed of 30 m/s (108 km/h), the radius of turn is 360 m. For a modern high speed train at 80 m/s, the toppling limit would be about 2.5 km. In practice, the minimum radius of turn is much greater than this, as contact between the wheel flanges and rail at high speed could cause significant damage to both. For very high speed, the minimum adhesion limit again appears appropriate, implying a radius of turn of about 13 km. In practice, curved lines used for high speed travel are superelevated or canted so that the turn limit is closer to 7 km.

During the 19th century, it was widely believed that coupling the drive wheels would compromise performance and was avoided on engines intended for express passenger service. With a single drive wheelset, the Herzian contact stress between the wheel and rail necessitated the largest diameter wheels that could be accommodated. The weight of locomotive was restricted by the stress on the rail and sandboxes were required, even under reasonable adhesion conditions.

Directional stability and hunting instability

While common belief dictates that the wheels are kept on the tracks by the flanges, the flanges in reality make few contacts with the track and, when they do, most of the contact is sliding. The rubbing of a flange on the track dissipates large amounts of energy, mainly as heat but also including noise and, if sustained, would lead to excessive wheel wear.

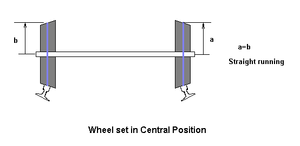
Close examination of a typical railway wheel reveals that the tread is burnished but the flange is not; the flanges rarely make contact with the rail. The tread of the wheel is slightly tapered. When the train is in the centre of the track, the region of the wheels in contact with the rail traces out a circle which has the same diameter for both wheels. The velocities of the two wheels are equal, so the train moves in a straight line.

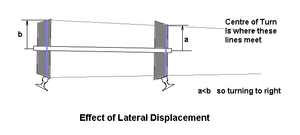
If, however, the wheelset is displaced to one side, the diameters of the regions of contact and hence the (linear) velocities of the wheels, are different and the wheelset tends to steer back towards the centre. Also, when the train encounters a bend, the wheelset displaces laterally slightly, so that the outer wheel speeds up (linearly) and the inner wheel slows down, causing the train to turn the corner. It should be noted that some railway systems employ a flat wheel and track profile, relying on cant alone to reduce flange contact, e.g. Melbourne suburban network, Australia.

Understanding how the train stays on the track, it becomes evident why Victorian locomotive engineers were averse to coupling wheelsets. This simple coning action is possible only with wheelsets where each can have some free motion about its vertical axis. If wheelsets are rigidly coupled together, this motion is restricted, so that coupling the wheels would be expected to introduce sliding, resulting in increased rolling losses. This problem was alleviated to a great extent by ensuring the diameter of all coupled wheels was very closely matched.

With perfect rolling contact between the wheel and rail, this coning behaviour manifests itself as a swaying of the train from side to side. In practice, the swaying is damped out below a critical speed, but is amplified by the forward motion of the train above the critical speed. This lateral swaying is known as 'hunting'. The phenomenon of hunting was known by the end of the 19th Century, although the cause was not fully understood until the 1920s and measures to eliminate it were not taken until the late 1960s. As is often the case, the limitation on maximum speed was imposed not by raw power but by encountering an instability in the motion.

The kinematic description of the motion of tapered treads on the two rails is insufficient to describe hunting well enough to predict the critical speed. It is necessary to deal with the forces involved. There are two phenomena which must be taken into account. The first is the inertia of the wheelsets and vehicle bodies, giving rise to forces proportional to acceleration; the second is the distortion of the wheel and track at the point of contact, giving rise to elastic forces. The kinematic approximation corresponds to the case which is dominated by contact forces.

A fairly straightforward analysis of the kinematics of the coning action yields an estimate of the wavelength of the lateral oscillation:

$\lambda=\frac{1}{2\pi}\sqrt{\frac{rd}{2k}}$

where d is the wheel gauge, r is the nominal wheel radius and k is the taper of the treads. For a given speed, the longer the wavelength and the lower the inertial forces will be, so the more likely it is that the oscillation will be damped out. Since the wavelength increases with reducing taper, increasing the critical speed requires the taper to be reduced, which implies a large minimum radius of turn.

A more complete analysis, taking account of the actual forces acting, yields the following result for the critical speed of a wheelset:

$V^2=\frac{Wrad^2}{k \left(4C+md^2 \right)}$

where W is the axle load for the wheelset, a is a shape factor related to the amount of wear on the wheel and rail, C is the moment of inertia of the wheelset perpendicular to the axle, m is the wheelset mass.

The result is consistent with the kinematic result in that the critical speed depends inversely on the taper. It also implies that the weight of the rotating mass should be minimised compared with the weight of the vehicle. The wheel gauge implicitly appears in both the numerator and denominator, implying that it has only a second-order effect on the critical speed.

The true situation is much more complicated, as the response of the vehicle suspension must be taken into account. Restraining springs, opposing the yaw motion of the wheelset, and similar restraints on bogies, may be used to raise the critical speed further. However, in order to achieve the highest speeds without encountering instability, a significant reduction in wheel taper is necessary, so there is little prospect of reducing the turn radius of high speed trains much below the current value of 7 km.

Forces on wheels

The behaviour of adhesion railways is determined by the forces arising between two surfaces in contact. This may appear trivially simple from a superficial glance but it becomes extremely complex when studied to the depth necessary to predict useful results.

The first error to address is the assumption that wheels are round. A glance at a parked car will immediately show that this is not true; the region in contact with the road is noticeably flattened, so that the wheel and road conform to each other over a region of contact. If this were not the case, the contact stress of a load being transferred through a point contact would be infinite. Rails and railway wheels are much stiffer than pneumatic tyres and tarmac but the same distortion takes place at the region of contact. Typically, the area of contact is elliptical, of the order of 15 mm across.

The distortion is small and localised but the forces which arise from it are large. In addition to the distortion due to the weight, both wheel and rail distort when braking and accelerating forces are applied and when the vehicle is subjected to side forces. These tangential forces cause distortion in the region where they first come into contact, followed by a region of slippage. The net result is that, during traction, the wheel does not advance as far as would be expected from rolling contact but, during braking, it advances further. This mix of elastic distortion and local slipping is known as "creep" (not to be confused with the creep of materials under constant load). The definition of creep in this context is:

$\mbox{creep}=\frac{(\mbox{actual displacement} - \mbox{rolling displacement})}{(\mbox{rolling displacement})} \,$

In analysing the dynamics of wheelsets and complete rail vehicles, the contact forces are treated as linearly dependent on the creep.

The forces which result in directional stability, propulsion and braking may all be traced to creep. It is present in a single wheelset and will accommodate the slight kinematic incompatibility introduced by coupling wheelsets together, without causing gross slippage, as was once feared.

Provided the radius of turn is sufficiently great (as should be expected for express passenger services), two or three linked wheelsets should not present a problem. However, 10 drive wheels (5 main wheelsets) are usually associated with heavy freight locomotives.

Booster

Some steam locomotives were fitted with booster engines on the rear trailing wheels. These were turned on as required at starting to give additional adhesive effort.

See also

• Friction
• Rolling resistance
• Slippery rail
• Traction
• Wrong kind of snow
• Wheelset

References

1. ^ http://www.rail-info.ch/BOB/index.en.html
2. ^ http://documents.epfl.ch/users/a/al/allenbac/www/documents/ResuTE31.pdf

• Inglis, Sir Charles (1951). Applied Mathematics for Engineers. Cambridge University Press. pp. 194–195. 
• Carter, F W (July 25, 1928). On the Stability of Running of Locomotives. Proc. Royal Society. 
• Wickens, A H (1965–1966). "The Dynamics of Railway Vehicles on Straight Track: Fundamental Considerations of Lateral Stability". Proc. Inst. Mech. Eng.: 29. 
• Wickens, A H; Gilchrist, A O; Hobbs, A E W (1969–1970). Proc. Inst. Mech. Eng.. p. 22.