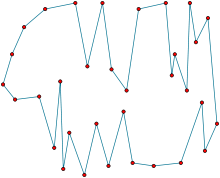
Bitonic tour

Bitonic tour
A bitonic tour

In computational geometry, a bitonic tour of a set of point sites in the Euclidean plane is a closed polygonal chain that has each site as one of its vertices, such that any vertical line crosses the chain at most twice.

The optimal bitonic tour is a bitonic tour of minimum total length. It is a standard exercise in dynamic programming to devise a polynomial time algorithm that constructs the optimal bitonic tour.[1] The optimal bitonic tour may be used as a heuristic solution to the traveling salesman problem, however its length may be larger than that of the optimal traveling salesman tour.[2]

At the 5th International Olympiad in Informatics, in Mendoza, Argentina in 1993, one of the contest problems involved bitonic tours: the contestants were to devise an algorithm that took as input a set of sites and a collection of allowed edges between sites and construct a bitonic tour using those edges that included as many sites as possible. As with the optimal bitonic tour, this problem may be solved by dynamic programming.[3]

The optimal bitonic tour has no self-crossings, because any two edges that cross can be replaced by an uncrossed pair of edges with shorter total length.

References

  1. ^ Introduction to Algorithms, 2nd ed., T. H. Cormen, C. E. Leiserson, R. Rivest, and C. Stein, MIT Press, 2001. Problem 15-1, p. 364.
  2. ^ Bentley, Jon L. (1990), "Experiments on traveling salesman heuristics", Proc. 1st ACM-SIAM Symp. Discrete Algorithms (SODA), pp. 91–99, http://portal.acm.org/citation.cfm?id=320186 .
  3. ^ IOI'93 contest problems and report.


Stub icon This geometry-related article is a stub. You can help Wikipedia by expanding it.