Dominance order

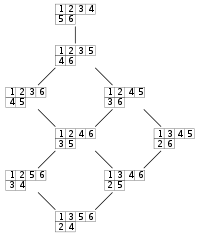
Example of dominance ordering of partitions of n. Here, n = 6, nodes are partitions of 6, edges indicate that the upper node dominates the lower node. While this particular partial ordering is graded, this is not true for the dominance ordering on partitions of any number n > 6.

Dominance order (synonyms: dominance ordering, majorization order, natural ordering) is a partial order on the set of partitions of a positive integer n that plays an important role in algebraic combinatorics and representation theory, especially in the context of symmetric functions and representation theory of the symmetric group.

Definition

If p₁,p₂,… and q₁,q₂,… are partitions of n, with the parts arranged in the weakly decreasing order, then p precedes q in the dominance order if for any k ≥ 1, the sum of the k largest parts of p is less than or equal to the sum of the k largest parts of q:

$p\trianglelefteq q$ if and only if $p_1+\cdots+p_k \leq q_1+\cdots+q_k$ for all $k\geq 1.$

In this definition, partitions are extended by appending zero parts at the end as necessary.

Properties of the dominance ordering

• Among the partitions of n, (1,…,1) is the smallest and (n) is the largest.
• The dominance ordering implies lexicographical ordering, i.e. if p dominates q, then p_i $\geq$ q_i for all i.
• The poset of partitions of n is linearly ordered (and is equivalent to lexicographical ordering) if and only if n ≤ 5. It is graded if and only if n ≤ 6. See image at right for an example.
• A partition p covers a partition q if and only if p_i = q_i + 1, p_k = q_k − 1, p_j = q_j for all j ≠ i,k and either (1) k = i + 1 or (2) q_i = q_k (Brylawski, Prop. 2.3). Starting from the Young diagram of q, the Young diagram of p is obtained from it by first removing the last box of row k and then appending it either to the end of the immediately preceding row k − 1, or to the end of row i < k if the rows i through k of the Young diagram of q all have the same length.
• Every partition p has a conjugate (or dual) partition p′, whose Young diagram is the transpose of the Young diagram of p. This operation reverses the dominance ordering:

$p\trianglelefteq q$ if and only if $q^{\prime}\trianglelefteq p^{\prime}.$

• The dominance ordering determines the inclusions between the Zariski closures of the conjugacy classes of nilpotent matrices.

Lattice structure

Partitions of n form a lattice under the dominance ordering, denoted L_n, and the operation of conjugation is an antiautomorphism of this lattice. To explicitly describe the lattice operations, for each partition p consider the associated (n+1)-tuple:

$\hat{p}=(0, p_1, p_1+p_2, \ldots, p_1+p_2+\ldots+p_n).$

The partition p can be recovered from its associated (n+1)-tuple by applying the step 1 difference, $p_i=\hat{p}_i-\hat{p}_{i-1}.$ Moreover, the (n+1)-tuples associated to partitions of n are characterized among all integer sequences of length n+1 by the following three properties:

• Nondecreasing, $\hat{p}_i\leq \hat{p}_{i+1};$
• Concave, $2\hat{p}_i\geq \hat{p}_{i-1}+\hat{p}_{i+1};$
• The initial term is 0 and the final term is n, $\hat{p}_0=0, \hat{p}_n=n.$

By the definition of the dominance ordering, partition p precedes partition q if and only if the associated (n+1)-tuple of p is term-by-term less than or equal to the associated (n + 1)-tuple of q. If p, q, r are partitions then $r\trianglelefteq p, r\trianglelefteq q$ if and only if $\hat{r}\leq\hat{p}, \hat{r}\leq\hat{q}.$ The componentwise minimum of two nondecreasing concave integer sequences is also nondecreasing and concave. Therefore, for any two partitions of n, p and q, their meet is the partition of n whose associated (n + 1)-tuple has components $\operatorname{min}(\hat{p}_i,\hat{q}_i).$ The natural idea to use a similar formula for the join fails, because the componentwise maximum of two concave sequences need not be concave. For example, for n=6, the partitions [3,1,1,1] and [2,2,2] have associated sequences (0,3,4,5,6,6,6) and (0,2,4,6,6,6,6), whose componentwise maximum (0,3,4,6,6,6,6) does not correspond to any partition. To show that any two partitions of n have a join, one uses the conjugation antiautomorphism: the join of p and q is the conjugate partition of the meet of p′ and q′:

$p\lor q=(p^{\prime} \land q^{\prime})^{\prime}.$

For the two partitions p and q in the preceding example, their conjugate partitions are [4,1,1] and [3,3] with meet [3,2,1], which is self-conjugate; therefore, the join of p and q is [3,2,1].

Thomas Brylawski has determined many invariants of the lattice L_n, such as the minimal height and the maximal covering number, and classified the intervals of small length. While L_n is not distributive for n ≥ 7, it shares some properties with distributive lattices: for example, its Möbius function takes on only values 0, 1, −1.

Generalizations

The dominance order on Young tableaux for the partition 6 = 4+2

Partitions of n can be graphically represented by Young diagrams on n boxes. Standard Young tableaux are certain ways to fill Young diagrams with numbers, and a partial order on them (sometimes called the dominance order on Young tableaux) can be defined in terms of the dominance order on the Young diagrams. For a Young tableau T to dominate another Young tableau S, the shape of T must dominate that of S as a partition, and moreover the same must hold whenever T and S are first truncated to their sub-tableaux containing entries up to a given value k, for each choice of k.

Similarly, there is a dominance order on the set of standard Young bitableaux, which plays a role in the theory of standard monomials.

See also

• Young's lattice
• Majorization

References

• Ian G. Macdonald, Symmetric functions and Hall polynomials, Oxford University Press, 1979, ISBN 0-19-853530-9 (See section I.1, pp. 5-7)
• Richard P. Stanley, Enumerative Combinatorics, Volume 2. Cambridge University Press, 1999 ISBN 0-521-56069-1
• Thomas Brylawski, The lattice of integer partitions, Discrete Mathematics, vol. 6, no. 3, 1973, pp. 201–219