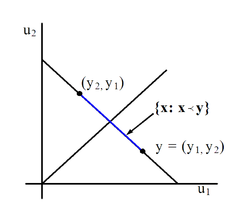- Majorization
-
This article is about a partial ordering of vectors on Rd. For functions, see Lorenz ordering.
In mathematics, majorization is a partial order on vectors of real numbers. For a vector
 , we denote by
, we denote by  the vector with the same components, but sorted in decreasing order. Given
the vector with the same components, but sorted in decreasing order. Given  , we say that
, we say that  weakly majorizes (or dominates)
weakly majorizes (or dominates)  written as
written as  iff
iffwhere
 and
and  are the elements of
are the elements of  and
and  , respectively, sorted in decreasing order. Equivalently, we say that
, respectively, sorted in decreasing order. Equivalently, we say that  is weakly majorized (or dominated) by
is weakly majorized (or dominated) by  , denoted as
, denoted as  .
.If
 and in addition
and in addition  we say that
we say that  majorizes (or dominates)
majorizes (or dominates)  written as
written as  . Equivalently, we say that
. Equivalently, we say that  is majorized (or dominated) by
is majorized (or dominated) by  , denoted as
, denoted as  .
.Regrettably, to confuse the matter, some literature sources use the reverse notation, e.g.,
 is replaced with
is replaced with  , most notably, in Horn and Johnson, Matrix analysis (Cambridge Univ. Press, 1985), Definition 4.3.24, while the same authors switch to the traditional notation, introduced here, later in their Topics in Matrix Analysis (1994).
, most notably, in Horn and Johnson, Matrix analysis (Cambridge Univ. Press, 1985), Definition 4.3.24, while the same authors switch to the traditional notation, introduced here, later in their Topics in Matrix Analysis (1994).A function
 is said to be Schur convex when
is said to be Schur convex when  implies
implies  . Similarly,
. Similarly,  is Schur concave when
is Schur concave when  implies
implies 
The majorization partial order on finite sets, described here, can be generalized to the Lorenz ordering, a partial order on distribution functions.
Contents
Examples
The order of the entries does not affect the majorization, e.g., the statement
 is simply equivalent to
is simply equivalent to  .
.(Strong) majorization:
 . For vectors with n components
. For vectors with n components(Weak) majorization:
 . For vectors with n components:
. For vectors with n components:Geometry of Majorization
For
 we have
we have  if and only if
if and only if  is in the convex hull of all vectors obtained by permuting the coordinates of
is in the convex hull of all vectors obtained by permuting the coordinates of  .
.Figure 1 displays the convex hull in 2D for the vector
 . Notice that the center of the convex hull, which is an interval in this case, is the vector
. Notice that the center of the convex hull, which is an interval in this case, is the vector  . This is the "smallest" vector satisfying
. This is the "smallest" vector satisfying  for this given vector
for this given vector  .
.Figure 2 shows the convex hull in 3D. The center of the convex hull, which is a 2D polygon in this case, is the "smallest" vector
 satisfying
satisfying  for this given vector
for this given vector  .
.Equivalent conditions
Each of the following statements is true if and only if
 :
: for some doubly stochastic matrix D (see Arnold,[1] Theorem 2.1).
for some doubly stochastic matrix D (see Arnold,[1] Theorem 2.1).- From
 we can produce
we can produce  by a finite sequence of "Robin Hood operations" where we replace two elements ai and aj < ai with ai − ε and aj + ε, respectively, for some
by a finite sequence of "Robin Hood operations" where we replace two elements ai and aj < ai with ai − ε and aj + ε, respectively, for some  (see Arnold,[1] p. 11).
(see Arnold,[1] p. 11). - For every convex function
 ,
,  (see Arnold,[1] Theorem 2.9).
(see Arnold,[1] Theorem 2.9).  . (see Nielsen and Chuang Exercise 12.17,[2])
. (see Nielsen and Chuang Exercise 12.17,[2])
In linear algebra
- Suppose that for two real vectors
 , v majorizes v'. Then it can be shown that there exists a set of probabilities
, v majorizes v'. Then it can be shown that there exists a set of probabilities  and a set of permutations
and a set of permutations  such that
such that  . Alternatively it can be shown that there exists a doubly stochastic matrix D such that vD = v'
. Alternatively it can be shown that there exists a doubly stochastic matrix D such that vD = v'
- We say that a hermitian operator, H, majorizes another, H', if the set of eigenvalues of H majorizes that of H'.
In recursion theory
Given
 , then
, then  is said to majorize
is said to majorize  if, for all
if, for all  ,
,  . If there is some
. If there is some  so that
so that  for all
for all  , then
, then  is said to dominate (or eventually dominate)
is said to dominate (or eventually dominate)  . Alternatively, the preceding terms are often defined requiring the strict inequality
. Alternatively, the preceding terms are often defined requiring the strict inequality  instead of
instead of  in the foregoing definitions.
in the foregoing definitions.See also
- For positive integer numbers, weak majorization is called Dominance order.
Notes
- ^ a b c Barry C. Arnold. "Majorization and the Lorenz Order: A Brief Introduction". Springer-Verlag Lecture Notes in Statistics, vol. 43, 1987.
- ^ Nielsen and Chuang. "Quantum Computation and Quantum Information". Cambridge University Press, 2000
References
- J. Karamata. Sur une inegalite relative aux fonctions convexes. Publ. Math. Univ. Belgrade 1, 145–158, 1932.
- G. H. Hardy, J. E. Littlewood and G. Pólya, Inequalities, 2nd edition, 1952, Cambridge University Press, London.
- Inequalities: Theory of Majorization and Its Applications (In preparation) Albert W. Marshall, Ingram Olkin, Barry Arnold, ISBN 9780387400877
- Inequalities: Theory of Majorization and Its Applications (1980) Albert W. Marshall, Ingram Olkin, Academic Press, ISBN 9780124737501
- A tribute to Marshall and Olkin's book "Inequalities: Theory of Majorization and its Applications"
- Quantum Computation and Quantum Information, (2000) Michael A. Nielsen and Isaac L. Chuang, Cambridge University Press, ISBN 9780521635035
- Matrix Analysis (1996) Rajendra Bhatia, Springer, ISBN 9780387948461
- Topics in Matrix Analysis (1994) Roger A. Horn and Charles R. Johnson, Cambridge University Press, ISBN 9780521467131
- Majorization and Matrix Monotone Functions in Wireless Communications (2007) Eduard Jorswieck and Holger Boche, Now Publishers, ISBN 9781601980403
- The Cauchy Schwarz Master Class (2004) J. Michael Steele, Cambridge University Press, ISBN 9780521546775
External links
Software
Categories:
Wikimedia Foundation. 2010.