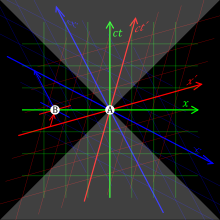
Consequences of special relativity

Special relativity has several consequences that struck many people as counterintuitive, among which are:

• The time lapse between two events is not invariant from one observer to another, but is dependent on the relative speeds of the observers' reference frames. (See Lorentz transformation equations.)
• Two events that occur simultaneously in different places in one frame of reference may occur at different times in another frame of reference (lack of absolute simultaneity).
• The dimensions (e.g. length, see Length contraction) of an object as measured by one observer may differ from the results of measurements of the same object made by another observer. (See Lorentz transformation equations.)
• The twin paradox concerns a twin who flies off in a spaceship traveling near the speed of light. When he returns he discovers that his twin has aged much more rapidly than he has (or he aged more slowly).
• The ladder paradox involves a long ladder traveling near the speed of light and being contained within a smaller garage.
• Velocities do not combine by simple addition, but instead by a relativistic velocity addition formula.
• Fast moving objects will appear to be distorted by Terrell rotation.
• The inability for matter or information to travel faster-than-light.

The effect on time

The assumption that light travels at a constant speed in a vacuum has a distinct effect on time.

Imagine a clock that measured time by bouncing a photon (a particle of light) between two mirrors that are its walls, say "horizontally". The photon must always travel at the speed of light (c). Even when the clock is moving (at velocity v_clock), the light photon must move at exactly the speed of light. Now if the direction the clock is moving is "vertical" (perpendicular to the original path of the photon), the photon's velocity can be represented by a vector whose direction is the hypotenuse of the right triangle formed by the horizontal (v_photon) and vertical (v_clock) components. Since the length of this hypotenuse (the resultant velocity) must not exceed c, the "horizontal" speed of the photon (the length of v_photon) will be less than c. This can be determined using the Pythagorean theorem (a² + b² = c²):

$v_\mathrm{photon}^2+v_\mathrm{clock}^2=c^2$

which can be solved as:

$v_\mathrm{photon}=\sqrt{c^2-v_\mathrm{clock}^2}$ .

To check, substituting 0 for v_clock makes:

v_photon = c   (which makes sense).

If the distance between the clock mirrors were w_clock and the clock were not moving, then based on the definition of speed, the photon would travel once between the mirrors in the amount of time, t_stationary, given by:

t_stationary = distance / speed = w_clock / c .

t_stationary is the time interval measured by the stationary clock—its basic unit (or "tick" interval).

However, if the clock were moving, then the "horizontal" speed of the photon towards the opposite mirror (v_photon) calculated above would be $\sqrt{c^2-v_\mathrm{clock}^2}$. Hence, the time interval measured by the moving clock will be:

$t_\mathrm{moving}=w_\mathrm{clock}/\sqrt{c^2-v_\mathrm{clock}^2}$

(Note that the above works because w_clock is the ("horizontal") width of the clock in a dimension in which it is not moving, and the clock's width is not relativistically affected by the movement in an orthogonal dimension.)

Since we want to know the effect of moving the clock on its basic time interval, we rearrange the equation, t_stationary = w_clock / c to:

$w_\mathrm{clock}=t_\mathrm{stationary}\cdot c$

and substitute that into the equation above to get:

$t_\mathrm{moving}=t_\mathrm{stationary}\cdot c/\sqrt{c^2-v_\mathrm{clock}^2}$.

c can be factored out of the denominator by factoring the c² out of the $(c^2-v_\mathrm{clock}^2)$ to get $\sqrt{c^2(1-v_\mathrm{clock}^2/c^2)}$ which leads to $c\cdot \sqrt{1-v_\mathrm{clock}^2/c^2}$. The c's in the numerator and the denominator then cancel out to make

$t_\mathrm{moving}=t_\mathrm{stationary}/\sqrt{1-v_\mathrm{clock}^2/c^2} = \gamma \cdot t_\mathrm{stationary}$

where $\gamma = 1 / \sqrt{1-v_\mathrm{clock}^2/c^2}$ is known as the Lorentz factor.

This means that the faster the clock moves, the longer its "tick interval" relative to a stationary clock. In effect, time measured by the moving clock has slowed down!

Extrapolating this, because all motion is relative, if ship A is moving relative to ship B, occupants of ship A see the time of occupants of ship B running slow and occupants of ship B see the time of occupants of ship A running slow. There is no logical or experimental way of saying which occupants are "right", so they can both be said to be correct.

Simultaneity

Event B is simultaneous with A in the green reference frame, but it occurred before in the blue frame, and will occur later in the red frame.

Main article: Relativity of simultaneity

From the first equation of the Lorentz transformation in terms of coordinate differences

$\Delta t' = \gamma \left(\Delta t - \frac{v \,\Delta x}{c^{2}} \right)$

it is clear that two events that are simultaneous in frame S (satisfying Δt = 0), are not necessarily simultaneous in another inertial frame S′ (satisfying Δt′ = 0). Only if these events are colocal in frame S (satisfying Δx = 0), will they be simultaneous in another frame S′.

Time dilation and length contraction

See also: Twin paradox

Writing the Lorentz transformation and its inverse in terms of coordinate differences we get

$\begin{cases} \Delta t' = \gamma \left(\Delta t - \frac{v \,\Delta x}{c^{2}} \right) \\ \Delta x' = \gamma (\Delta x - v \,\Delta t)\, \end{cases}$

and

$\begin{cases} \Delta t = \gamma \left(\Delta t' + \frac{v \,\Delta x'}{c^{2}} \right) \\ \Delta x = \gamma (\Delta x' + v \,\Delta t')\, \end{cases}$

Suppose we have a clock at rest in the unprimed system S. Two consecutive ticks of this clock are then characterized by Δx = 0. If we want to know the relation between the times between these ticks as measured in both systems, we can use the first equation and find:

$\Delta t' = \gamma\, \Delta t \qquad ( \,$ for events satisfying $\Delta x = 0 )\,$

This shows that the time Δt' between the two ticks as seen in the 'moving' frame S' is larger than the time Δt between these ticks as measured in the rest frame of the clock. This phenomenon is called time dilation. Time dilation explains a number of physical phenomena; for example, the decay rate of muons produced by cosmic rays impinging on the Earth's atmosphere.^[1]

Similarly, suppose we have a measuring rod at rest in the unprimed system. In this system, the length of this rod is written as Δx. If we want to find the length of this rod as measured in the 'moving' system S', we must make sure to measure the distances x' to the end points of the rod simultaneously in the primed frame S'. In other words, the measurement is characterized by Δt' = 0, which we can combine with the fourth equation to find the relation between the lengths Δx and Δx':

$\Delta x' = \frac{\Delta x}{\gamma} \qquad ( \,$ for events satisfying $\Delta t' = 0 )\,$

This shows that the length Δx' of the rod as measured in the 'moving' frame S' is shorter than the length Δx in its own rest frame. This phenomenon is called length contraction or Lorentz contraction.

These effects are not merely appearances; they are explicitly related to our way of measuring time intervals between events which occur at the same place in a given coordinate system (called "co-local" events). These time intervals will be different in another coordinate system moving with respect to the first, unless the events are also simultaneous. Similarly, these effects also relate to our measured distances between separated but simultaneous events in a given coordinate system of choice. If these events are not co-local, but are separated by distance (space), they will not occur at the same spatial distance from each other when seen from another moving coordinate system. However, the space-time interval will be the same for all observers. The underlying reality remains the same. Only our perspective changes.

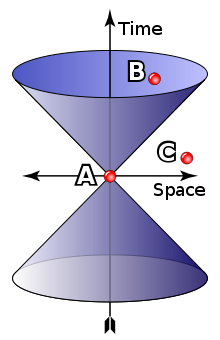
Causality and prohibition of motion faster than light

Diagram 2. Light cone

In diagram 2 the interval AB is 'time-like'; i.e., there is a frame of reference in which events A and B occur at the same location in space, separated only by occurring at different times. If A precedes B in that frame, then A precedes B in all frames. It is hypothetically possible for matter (or information) to travel from A to B, so there can be a causal relationship (with A the cause and B the effect).

The interval AC in the diagram is 'space-like'; i.e., there is a frame of reference in which events A and C occur simultaneously, separated only in space. However there are also frames in which A precedes C (as shown) and frames in which C precedes A. If it were possible for a cause-and-effect relationship to exist between events A and C, then special relativity would be falsified. Otherwise paradoxes of causality would result. For example, if A was the cause, and C the effect, then there would be frames of reference in which the effect preceded the cause. Although this in itself won't give rise to a paradox, one can show^[2][3] that in special relativity faster than light signals can be sent back into one's own past. A causal paradox can then be constructed by sending the signal if and only if no signal was received previously.

Therefore, to preserve causality one of the assumptions of special relativity is that, no information or material object can travel faster than light. On the other hand, the logical situation is not as clear in the case of general relativity, so it is an open question whether there is a fundamental mechanism that prevents motion faster than light (and therefore preserves causality) in general relativity.

Even without considerations of causality, there are other strong reasons why faster-than-light travel would falsify special relativity. For example, if a constant force is applied to an object for a limitless amount of time, then integrating F = dp/dt gives a momentum that grows without bound, but this is simply because $p = m \gamma v \,$ approaches infinity as v approaches c. To an observer who is not accelerating, it appears as though the object's inertia is increasing, so as to produce a smaller acceleration in response to the same force. This behavior is in fact observed in particle accelerators.

Composition of velocities

Main article: Velocity-addition formula

If the observer in S sees an object moving along the x axis at velocity w, then the observer in the S' system, a frame of reference moving at velocity v in the x direction with respect to S, will see the object moving with velocity w' where

$w'=\frac{w-v}{1-wv/c^2}.$

This equation can be derived from the space and time transformations above.

$w'=\frac{dx'}{dt'}=\frac{\gamma(dx-v dt)}{\gamma(dt-v dx/c^2)}=\frac{(dx/dt)-v}{1-(v/c^2)(dx/dt)}$

Notice that if the object were moving at the speed of light in the S system (i.e. w = c), then it would also be moving at the speed of light in the S' system. Also, if both w and v are small with respect to the speed of light, we will recover the intuitive Galilean transformation of velocities: $w' \approx w-v$.

The usual example given is that of a train (call it system K) travelling due east with a velocity v with respect to the tracks (system K'). A child inside the train throws a baseball due east with a velocity u with respect to the train. In classical physics, an observer at rest on the tracks will measure the velocity of the baseball as v + u. In special relativity, this is no longer true. Instead, an observer on the tracks will measure the velocity of the baseball as $\frac{v+u}{1+\frac{vu}{c^2}}$. If u and v are small compared to c, then the above expression approaches the classical sum v + u.

A more general formula can be derived if the baseball is no longer assumed to travel in a direction parallel to the motion of the train. Einstein's addition of colinear velocites is consistent with the Fizeau experiment which determined the speed of light in a fluid moving parallel to the light, but no experiment has ever tested the formula for the general case of non-parallel velocities.^{[citation needed]}

References

1. ^ Kleppner, Daniel; Kolenkow, David (1973). An Introduction to Mechanics. pp. 468–70. 
2. ^ R. C. Tolman, The theory of the Relativity of Motion, (Berkeley 1917), p. 54
3. ^ G. A. Benford, D. L. Book, and W. A. Newcomb, The Tachyonic Antitelephone, Phys. Rev. D 2, 263–265 (1970) article