- Mittag-Leffler star
-
In complex analysis, a branch of mathematics, the Mittag-Leffler star of a complex-analytic function is a set in the complex plane obtained by attempting to extend that function along rays emanating from a given point. This concept is named after Gösta Mittag-Leffler.
Contents
Definition and elementary properties
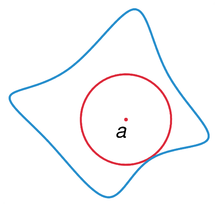
Formally, the Mittag-Leffler star of a complex-analytic function ƒ defined on an open disk U in the complex plane centered at a point a is the set of all points z in the complex plane such that ƒ can be continued analytically along the line segment joining a and z (see analytic continuation along a curve).
It follows from the definition that the Mittag-Leffler star is an open star-convex set (with respect to the point a) and that it contains the disk U. Moreover, ƒ admits a single-valued analytic continuation to the Mittag-Leffler star.
Examples
- The Mittag-Leffler star of the complex exponential function defined in a neighborhood of a = 0 is the entire complex plane.
- The Mittag-Leffler star of the complex logarithm defined in the neighborhood of point a = 1 is the entire complex plane without the origin and the negative real axis. In general, given the complex logarithm defined in the neighborhood of a point a ≠ 0 in the complex plane, this function can be extended all the way to infinity on any ray starting at a, except on the ray which goes from a to the origin, one cannot extend the complex logarithm beyond the origin along that ray.
- Any open star-convex set is the Mittag-Leffler star of some complex-analytic function, since any open set in the complex plane is a domain of holomorphy.
Uses
Any complex-analytic function ƒ defined around a point a in the complex plane can be expanded in a series of polynomials which is convergent in the entire Mittag-Leffler star of ƒ at a. Each polynomial in this series is a linear combination of the first several terms in the Taylor series expansion of ƒ around a.
Such a series expansion of ƒ, called the Mittag-Leffler expansion, is convergent in a larger set than the Taylor series expansion of ƒ at a. Indeed, the largest open set on which the latter series is convergent is a disk centered at a and contained within the Mittag-Leffler star of ƒ at a
References
- Shenitzer, Abe; Stillwell, John; editors (2002). Mathematical evolutions. Washington, DC: Mathematical Association of America. pp. page 32. ISBN 0883855364.
- Korevaar, Jacob (2004). Tauberian theory: a century of developments. Berlin; New York: Springer. ISBN 354021058X.
External links
Categories:
Wikimedia Foundation. 2010.