Dual cone and polar cone

A set C and its dual cone C ^* .

A set C and its polar cone C^o. The dual cone and the polar cone are symmetric to each other with respect to the origin.

Dual cone and polar cone are closely related concepts in convex analysis, a branch of mathematics.

Dual cone

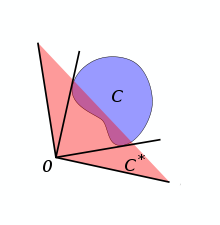
The dual cone C ^* of a subset C in a Euclidean space $\mathbb R^n$ is the set

$C^* = \left \{y\in \mathbb R^n: y \cdot x \geq 0 \quad \forall x\in C \right \},$

where "·" denotes the dot product.

C ^* is always a convex cone, even if C is neither convex nor a cone.

When C is a cone, the following properties hold:

• A non-zero vector y is in C ^* if and only if − y is the normal of a hyperplane that supports C at the origin.
• C ^* is closed and convex.
• $C_1 \subseteq C_2$ implies $C_2^* \subseteq C_1^*$.
• If C has nonempty interior, then C ^* is pointed, i.e. C ^* contains no line in its entirety.
• If C is a cone and the closure of C is pointed, then C ^* has nonempty interior.
• C ^{* *} is the closure of the smallest convex cone containing C.

A cone is said to be self-dual if C = C ^* . The nonnegative orthant of $\mathbb{R}^n$ and the space of all positive semidefinite matrices are self-dual.

Dual cones can be more generally defined on real Hilbert spaces.

Polar cone

The polar of the closed convex cone C is the closed convex cone C^o, and vice-versa.

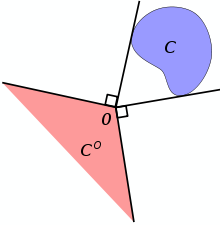
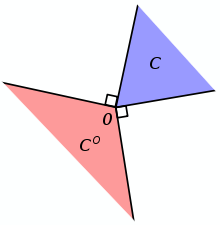
For a set C in $\mathbb R^n,$ the polar cone of C is the set

$C^o = \left \{y\in \mathbb R^n: y \cdot x \leq 0 \quad \forall x\in C \right \}.$

It is easy to check that C^o = − C ^* for any set C in $\mathbb R^n,$ and that the polar cone shares many of the properties of the dual cone.

References

• Goh, C. J.; Yang, X.Q. (2002). Duality in optimization and variational inequalities. London; New York: Taylor & Francis. ISBN 0415274796. 

• Boltyanski, V. G.; Martini, H., Soltan, P. (1997). Excursions into combinatorial geometry. New York: Springer. ISBN 3540613412. 

• Ramm, A.G.; Shivakumar, P.N.; Strauss, A.V. editors (2000). Operator theory and its applications. Providence, R.I.: American Mathematical Society. ISBN 0821819909.