Mollweide projection

Mollweide projection of the world.

The Mollweide projection with Tissot's indicatrix of deformation

The Mollweide projection is a pseudocylindrical map projection generally used for global maps of the world (or sky). Also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. As its more explicit name Mollweide equal area projection indicates, it sacrifices accuracy of angle and shape in favor of accurate depiction of area. It is used primarily where accurate representation of area takes precedence over shape, for instance small maps depicting global distributions.

The projection was first published by mathematician and astronomer Karl (or Carl) Brandan Mollweide (1774 – 1825) of Leipzig in 1805. It was popularized by Jacques Babinet in 1857, giving it the name homalographic projection. The variation homolographic arose from frequent nineteenth century usage in star atlases.^[1]

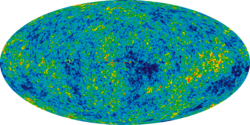Full-sky image of Cosmic Microwave Background as seen by the Wilkinson Microwave Anisotropy Probe. Projected using the Mollweide projection.

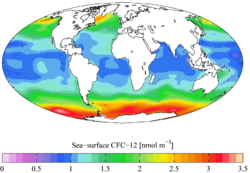Sea-surface freon levels measured by the Global Ocean Data Analysis Project. Projected using the Mollweide projection.

The projection is:

$x = \frac{2 \sqrt 2}{\pi} \lambda \cos\left(\theta \right),$

$y = \sqrt 2 \sin\left(\theta \right),\,$

where $\theta\,$ is an auxiliary angle defined by

$2 \theta + \sin(2 \theta) = \pi \sin(\phi)\qquad (1)$

and $\,\lambda$ is the longitude from the central meridian, and $\,\phi$ is the latitude.

Equation (1) may be solved with rapid convergence (but slow near the poles) using Newton–Raphson iteration:

$\theta_0 = \phi,\,$

$\theta_{n+1} = \theta_n - \frac{(2\theta_n + \sin(2\theta_n) - \pi \sin(\phi))}{2 + 2\cos(2\theta_n)}.\,$

If φ = ±π/2, then also θ = ±π/2. In that case the iteration should be bypassed; otherwise, division by zero may result.

Properties

The Mollweide is a pseudocylindrical projection in which the equator is represented as a straight horizontal line perpendicular to a central meridian one-half its length. The other parallels compress near the poles, while the other meridians are equally spaced at the equator. The meridians at 90 degrees east and west form a perfect circle, and the whole earth is depicted in a proportional 2:1 ellipse. The proportion of the area of the ellipse between any given parallel and the equator is the same as the proportion of the area on the globe between that parallel and the equator, but at the expense of shape distortion, which is significant at the perimeter of the ellipse, although not as severe as in the sinusoidal projection.

Shape distortion may be diminished by using an interrupted version. A sinusoidal interrupted Mollweide projection discards the central meridian in favor of alternating half-meridians which terminate at right angles to the equator. This has the effect of dividing the globe into lobes shape. In contrast, a parallel interrupted Mollweide projection uses multiple disjoint central meridians, giving the effect of multiple ellipses joined at the equator. More rarely, the project can be drawn obliquely to shift the areas of distortion to the oceans, allowing the continents to remain truer to form.

The Mollweide, or its properties, has inspired the creation of several other projections, including the Goode's homolosine, van der Grinten and the Boggs eumorphic.^[2]

See also

• Aitoff projection
• Hammer projection

References

1. ^ Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp. 112–113, ISBN 0-226-76747-7.
2. ^ Map Projections – A Working Manual, USGS Professional Paper 1395, John P. Snyder, 1987, pp. 249–252

External links

• An interactive JAVA applet to study deformations (area, distance and angle) of the Mollweide Map Projection
• Mollweide Projection at Mathworld