Subtraction

"5 − 2 = 3" (verbally, "five minus two equals three")

An example problem

Subtraction is one of the four basic binary arithmetic operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with. Subtraction is denoted by a minus sign in infix notation, in stark contrast to the use of the plus sign for addition.

Since subtraction is not a commuting operator, the two operands are named. The traditional names for the parts of the:c − b = a are minuend (c) − subtrahend (b) = difference (a). The words "minuend" and "subtrahend" are uncommon in modern usage.^[1] Instead we say that c and −b are terms, and treat subtraction as addition of the additive inverse. The answer is still called the difference.

Subtraction is used to model four related processes:

1. From a given collection, take away (subtract) a given number of objects. For example, 5 apples minus 2 apples leaves 3 apples.
2. From a given measurement, take away a quantity measured in the same units. If I weigh 200 pounds, and lose 10 pounds, then I weigh 200 − 10 = 190 pounds.
3. Compare two like quantities to find the difference between them. For example, the difference between $800 and $600 is $800 − $600 = $200. Also known as comparative subtraction.
4. To find the distance between two locations at a fixed distance from starting point. For example if, on a given highway, you see a mileage marker that says 150 miles and later see a mileage marker that says 160 miles, you have traveled 160 − 150 = 10 miles.

In mathematics, it is often useful to view or even define subtraction as a kind of addition, the addition of the additive inverse. We can view 7 − 3 = 4 as the sum of two terms: 7 and -3. This perspective allows us to apply to subtraction all of the familiar rules and nomenclature of addition. Subtraction is not associative or commutative—in fact, it is anticommutative and left-associative—but addition of signed numbers is both.

Basic subtraction: integers

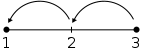
Imagine a line segment of length b with the left end labeled a and the right end labeled c. Starting from a, it takes b steps to the right to reach c. This movement to the right is modeled mathematically by addition:

a + b = c.

From c, it takes b steps to the left to get back to a. This movement to the left is modeled by subtraction:

c − b = a.

Now, imagine a line segment labeled with the numbers 1, 2, and 3. From position 3, it takes no steps to the left to stay at 3, so 3 − 0 = 3. It takes 2 steps to the left to get to position 1, so 3 − 2 = 1. This picture is inadequate to describe what would happen after going 3 steps to the left of position 3. To represent such an operation, the line must be extended.

To subtract arbitrary natural numbers, one begins with a line containing every natural number (0, 1, 2, 3, 4, 5, 6, ...). From 3, it takes 3 steps to the left to get to 0, so 3 − 3 = 0. But 3 − 4 is still invalid since it again leaves the line. The natural numbers are not a useful context for subtraction.

The solution is to consider the integer number line (..., −3, −2, −1, 0, 1, 2, 3, ...). From 3, it takes 4 steps to the left to get to −1:

3 − 4 = −1.

Subtraction as addition

There are some cases where subtraction as a separate operation becomes problematic. For example, 3 − (−2) (i.e. subtract −2 from 3) is not immediately obvious from either a natural number view or a number line view, because it is not immediately clear what it means to move −2 steps to the left or to take away −2 apples. One solution is to view subtraction as addition of signed numbers. Extra minus signs simply denote additive inversion. Then we have 3 − (−2) = 3 + 2 = 5. This also helps to keep the ring of integers "simple" by avoiding the introduction of "new" operators such as subtraction. Ordinarily a ring only has two operations defined on it; in the case of the integers, these are addition and multiplication. A ring already has the concept of additive inverses, but it does not have any notion of a separate subtraction operation, so the use of signed addition as subtraction allows us to apply the ring axioms to subtraction without needing to prove anything.

Algorithms for subtraction

There are various algorithms for subtraction, and they differ in their suitability for various applications. A number of methods are adapted to hand calculation; for example, when making change, no actual subtraction is performed, but rather the change-maker counts forward.

For machine calculation, the method of complements is preferred, whereby the subtraction is replaced by an addition in a modular arithmetic.

The method by which elementary school children are taught to subtract varies from country to country, and within a country, different methods are in fashion at different times. In traditional mathematics, a specific process is taught to children at the end of the 1st year or during the 2nd year for use with multi-digit whole numbers, and is extended in either the fourth or fifth grade to include decimal representations of fractional numbers.

American schools currently teach a method of subtraction using borrowing and a system of markings called crutches^{[citation needed]}. Although a method of borrowing had been known and published in textbooks prior, apparently the crutches are the invention of William A. Brownell who used them in a study in November 1937^{[citation needed]}. This system caught on rapidly, displacing the other methods of subtraction in use in America at that time.

European children are taught, and some older Americans employ a method of subtraction called the Austrian method, also known as the additions method. There is no borrowing in this method. There are also crutches (markings to aid the memory) which vary according to country^{[citation needed]}.

Both these methods break up the subtraction as a process of one digit subtractions by place value. Starting with a least significant digit, a subtraction of subtrahend:

s_j s_j−1 ... s₁

from minuend

m_k m_k−1 ... m₁,

where each s_i and m_i is a digit, proceeds by writing down m₁ − s₁, m₂ − s₂, and so forth, as long as s_i does not exceed m_i. Otherwise, m_i is increased by 10 and some other digit is modified to correct for this increase. The American method corrects by attempting to decrease the minuend digit m_i+1 by one (or continuing the borrow leftwards until there is a non-zero digit from which to borrow). The European method corrects by increasing the subtrahend digit s_i+1 by one.

Example: 704 − 512. The minuend is 704, the subtrahend is 512. The minuend digits are m₃ = 7, m₂ = 0 and m₁ = 4. The subtrahend digits are s₃ = 5, s₂ = 1 and s₁ = 2. Beginning at the one's place, 4 is not less than 2 so the difference 2 is written down in the result's one place. In the ten's place, 0 is less than 1, so the 0 is increased to 10, and the difference with 1, which is 9, is written down in the ten's place. The American method corrects for the increase of ten by reducing the digit in the minuend's hundreds place by one. That is, the 7 is struck through and replaced by a 6. The subtraction then proceeds in the hundreds place, where 6 is not less than 5, so the difference is written down in the result's hundred's place. We are now done, the result is 192.

The Austrian method will not reduce the 7 to 6. Rather it will increase the subtrahend hundred's digit by one. A small mark is made near or below this digit (depending on the school). Then the subtraction proceeds by asking what number when increased by 1, and 5 is added to it, makes 7. The answer is 1, and is written down in the result's hundred's place.

There is an additional subtlety in that the child always employs a mental subtraction table in the American method. The Austrian method often encourages the child to mentally use the addition table in reverse. In the example above, rather than adding 1 to 5, getting 6, and subtracting that from 7, the child is asked to consider what number, when increased by 1, and 5 is added to it, makes 7.

See also

• Elementary arithmetic
• Decrement
• Negative and non-negative numbers
• Method of complements

Notes and references

1. ^ *Linderholm, Carl (1971). Mathematics Made Difficult. Wolfe. p. 42. ISBN 0-7234-0415-1. 

• Browell, W. A. (1939). Learning as reorganization: An experimental study in third-grade arithmetic, Duke University Press.
• Subtraction in the United States: An Historical Perspective, Susan Ross, Mary Pratt-Cotter, The Mathematics Educator, Vol. 8, No. 1 (original publication) and Vol. 10, No. 1 (reprint.) http://math.coe.uga.edu/TME/Issues/v10n2/5ross.pdf

External links

Printable Worksheets: One Digit Subtraction, Two Digit Subtraction, and Four Digit Subtraction

• Subtraction Game at cut-the-knot
• Subtraction on a Japanese abacus selected from Abacus: Mystery of the Bead