Chordal graph

A cycle (black) with two chords (green). As for this part, the graph is chordal. However, removing one green edge would result in a non-chordal graph. Indeed, the other green edge with three black edges would form a cycle of length four with no chords.

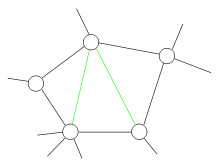
In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes. Some also state this as a chordal graph is a graph with no induced cycles of length more than three.

Chordal graphs are a subset of the perfect graphs. They are sometimes also called rigid circuit graphs^[1] or triangulated graphs, though the latter term is also used for maximal planar graphs.^[2]

Perfect elimination and efficient recognition

A perfect elimination ordering in a graph is an ordering of the vertices of the graph such that, for each vertex v, v and the neighbors of v that occur after v in the order form a clique. A graph is chordal if and only if it has a perfect elimination ordering (Fulkerson & Gross 1965).

Rose, Lueker & Tarjan (1976) (see also Habib et al. 2000) show that a perfect elimination ordering of a chordal graph may be found efficiently using an algorithm known as lexicographic breadth-first search. This algorithm maintains a partition of the vertices of the graph into a sequence of sets; initially this sequence consists of a single set with all vertices. The algorithm repeatedly chooses a vertex v from the earliest set in the sequence that contains previously-unchosen vertices, and splits each set S of the sequence into two smaller subsets, the first consisting of the neighbors of v in S and the second consisting of the non-neighbors. When this splitting process has been performed for all vertices, the sequence of sets has one vertex per set, in the reverse of a perfect elimination ordering.

Since both this lexicographic breadth first search process and the process of testing whether an ordering is a perfect elimination ordering can be performed in linear time, it is possible to recognize chordal graphs in linear time. The graph sandwich problem on chordal graphs is NP-complete (Bodlaender, Fellows & Warnow 1992), whereas the probe graph problem on chordal graphs has polynomial-time complexity (Berry, Golumbic & Lipshteyn 2007).

The set of all perfect elimination orderings of a chordal graph can be modeled as the basic words of an antimatroid; Chandran et al. (2003) use this connection to antimatroids as part of an algorithm for efficiently listing all perfect elimination orderings of a given chordal graph.

Maximal cliques and graph coloring

Another application of perfect elimination orderings is finding a maximum clique of a chordal graph in polynomial-time, while the same problem for general graphs is NP-complete. More generally, a chordal graph can have only linearly many maximal cliques, while non-chordal graphs may have exponentially many. To list all maximal cliques of a chordal graph, simply find a perfect elimination ordering, form a clique for each vertex v together with the neighbors of v that are later than v in the perfect elimination ordering, and test whether each of the resulting cliques is maximal.

The largest maximal clique is a maximum clique, and, as chordal graphs are perfect, the size of this clique equals the chromatic number of the chordal graph. Chordal graphs are perfectly orderable: an optimal coloring may be obtained by applying a greedy coloring algorithm to the vertices in the reverse of a perfect elimination ordering (Maffray 2003).

Minimal separators

In any graph, a vertex separator is a set of vertices the removal of which leaves the remaining graph disconnected; a separator is minimal if it has no proper subset that is also a separator. According to a theorem of Dirac (1961), the chordal graphs are exactly the graphs in which each minimal separator is a clique; Dirac used this characterization to prove that chordal graphs are perfect.

The family of chordal graphs may be defined inductively, as the graphs whose vertices can be divided into three nonempty subsets A, S, and B, such that A ∪ S and S ∪ B both form chordal induced subgraphs, S is a clique, and there are no edges from A to B. That is, they are the graphs that have a recursive decomposition by clique separators into smaller subgraphs. For this reason, chordal graphs have also sometimes been called decomposable graphs.^[3]

Intersection graphs of subtrees

A chordal graph with eight vertices, represented as the intersection graph of eight subtrees of a six-node tree.

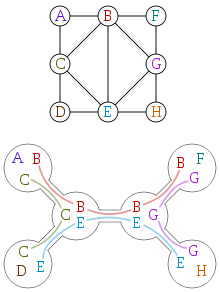
An alternative characterization of chordal graphs, due to Gavril (1974), involves trees and their subtrees.

From a collection of subtrees of a tree, one can define a subtree graph, which is an intersection graph that has one vertex per subtree and an edge connecting any two subtrees that overlap in one or more nodes of the tree. As Gavril showed, the subtree graphs are exactly the chordal graphs.

A representation of a chordal graph as an intersection of subtrees forms a tree decomposition of the graph, with treewidth equal to one less than the size of the largest clique in the graph; the tree decomposition of any graph G can be viewed in this way as a representation of G as a subgraph of a chordal graph. The tree decomposition of a graph is also the junction tree of the junction tree algorithm.

Relation to other graph classes

Subclasses

The interval graphs are the intersection graphs of subtrees of path graphs, a special case of trees; therefore, they are a subfamily of the chordal graphs.

The split graphs are exactly the graphs that are both chordal and the complements of chordal graphs. Bender, Richmond & Wormald (1985) showed that, in the limit as n goes to infinity, the fraction of n-vertex chordal graphs that are split approaches one.

The ptolemaic graphs, are exactly the graphs that are both chordal and distance-hereditary. The quasi-threshold graphs are a subclass of the ptolemaic graphs that are exactly the graphs that are both chordal and cographs. The block graphs are another subclass of ptolemaic graphs in which every two maximal cliques have at most one vertex in common. In a special case of the block graphs, the windmill graphs, the common vertex is the same for every pair of cliques.

The strongly chordal graphs are graphs that are chordal and contain no n-sun (n>=3) as induced subgraph.

The k-trees are the chordal graphs in which all maximal cliques and all maximal clique separators have the same size.^[4] The Apollonian networks are the chordal maximal planar graphs, or equivalently the planar 3-trees.^[4] The maximal outerplanar graphs are a subclass of 2-trees, and therefore are also chordal.

Superclasses

The chordal graphs are a subclass of the well known perfect graphs. Other superclasses of chordal graphs include the weakly chordal graphs, the odd-hole-free graphs, and the even-hole-free graphs. In fact, chordal graphs are precisely the graphs that are both odd-hole-free and even-hole-free (see holes in graph theory).

References

• Bender, E. A.; Richmond, L. B.; Wormald, N. C. (1985), "Almost all chordal graphs split", J. Austral. Math. Soc., Series A 38 (2): 214–221, doi:10.1017/S1446788700023077, MR0770128 .
• Berry, Anne; Golumbic, Martin Charles; Lipshteyn, Marina (2007), "Recognizing chordal probe graphs and cycle-bicolorable graphs", SIAM Journal on Discrete Mathematics 21 (3): 573–591, doi:10.1137/050637091 .
• Bodlaender, H. L.; Fellows, M. R.; Warnow, T. J. (1992), "Two strikes against perfect phylogeny", Proc. of 19th International Colloquium on Automata Languages and Programming .
• Chandran, L. S.; Ibarra, L.; Ruskey, F.; Sawada, J. (2003), "Enumerating and characterizing the perfect elimination orderings of a chordal graph", Theoretical Computer Science 307 (2): 303–317, doi:10.1016/S0304-3975(03)00221-4, http://www.cis.uoguelph.ca/~sawada/papers/chordal.pdf .
• Dirac, G. A. (1961), "On rigid circuit graphs", Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 25: 71–76, doi:10.1007/BF02992776, MR0130190 .
• Fulkerson, D. R.; Gross, O. A. (1965), "Incidence matrices and interval graphs", Pacific J. Math 15: 835–855, http://projecteuclid.org/Dienst/UI/1.0/Summarize/euclid.pjm/1102995572 .
• Gavril, Fănică (1974), "The intersection graphs of subtrees in trees are exactly the chordal graphs", Journal of Combinatorial Theory, Series B 16: 47–56, doi:10.1016/0095-8956(74)90094-X .
• Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press .
• Habib, Michel; McConnell, Ross; Paul, Christophe; Viennot, Laurent (2000), "Lex-BFS and partition refinement, with applications to transitive orientation, interval graph recognition, and consecutive ones testing", Theoretical Computer Science 234: 59–84, doi:10.1016/S0304-3975(97)00241-7, http://www.cs.colostate.edu/~rmm/lexbfs.ps .
• Maffray, Frédéric (2003), "On the coloration of perfect graphs", in Reed, Bruce A.; Sales, Cláudia L., Recent Advances in Algorithms and Combinatorics, CMS Books in Mathematics, 11, Springer-Verlag, pp. 65–84, doi:10.1007/0-387-22444-0_3, ISBN 0-387-95434-1 .
• Patil, H. P. (1986), "On the structure of k-trees", Journal of Combinatorics, Information and System Sciences 11 (2–4): 57–64, MR966069 .
• Rose, D.; Lueker, George; Tarjan, Robert E. (1976), "Algorithmic aspects of vertex elimination on graphs", SIAM Journal on Computing 5 (2): 266–283, doi:10.1137/0205021 .

Notes

1. ^ Dirac (1961).
2. ^ Weisstein, Eric W., "Triangulated Graph" from MathWorld.
3. ^ Peter Bartlett. "Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations:". http://www.stat.berkeley.edu/~bartlett/courses/241A-spring2007/graphnotes.pdf. 
4. ^ ^{a b} Patil (1986).

External links

• Information System on Graph Class Inclusions: chordal graph

• Weisstein, Eric W., "Chordal Graph" from MathWorld.