De Casteljau's algorithm

In the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau. De Casteljau's algorithm can also be used to split a single Bézier curve into two Bézier curves at an arbitrary parameter value.

Although the algorithm is slower for most architectures when compared with the direct approach, it is more numerically stable.

Definition

Given a polynomial B in Bernstein form of degree n

$B(t) = \sum_{i=0}^{n}\beta_{i}b_{i,n}(t),$

where b is a Bernstein basis polynomial, the polynomial at point t₀ can be evaluated with the recurrence relation

$\beta_i^{(0)} := \beta_i \mbox{ , } i=0,\ldots,n$

$\beta_i^{(j)} := \beta_i^{(j-1)} (1-t_0) + \beta_{i+1}^{(j-1)} t_0 \mbox{ , } i = 0,\ldots,n-j \mbox{ , } j= 1,\ldots,n$

Then, the evaluation of B at point t₀ can be evaluated in n steps of the algorithm. The result B(t₀) is given by :

$B(t_0)=\beta_0^{(n)}.$

Moreover, the Bézier curve B can be split at point t₀ into two curves with respective control points :

$\beta_0^{(0)},\beta_0^{(1)},\ldots,\beta_0^{(n)}$

$\beta_0^{(n)},\beta_1^{(n-1)},\ldots,\beta_n^{(0)}$

Example implementation

Here is an example implementation of De Casteljau's algorithm in Haskell:

deCasteljau :: Double -> [(Double, Double)] -> (Double, Double)
deCasteljau t [b] = b
deCasteljau t coefs = deCasteljau t reduced
  where
    reduced = zipWith (lerpP t) coefs (tail coefs)
    lerpP t (x0, y0) (x1, y1) = (lerp t x0 x1, lerp t y0 y1)
    lerp t a b = t * b + (1 - t) * a

Notes

When doing the calculation by hand it is useful to write down the coefficients in a triangle scheme as

$\begin{matrix} \beta_0 & = \beta_0^{(0)} & & & \\ & & \beta_0^{(1)} & & \\ \beta_1 & = \beta_1^{(0)} & & & \\ & & & \ddots & \\ \vdots & & \vdots & & \beta_0^{(n)} \\ & & & & \\ \beta_{n-1} & = \beta_{n-1}^{(0)} & & & \\ & & \beta_{n-1}^{(1)} & & \\ \beta_n & = \beta_n^{(0)} & & & \\ \end{matrix}$

When choosing a point t₀ to evaluate a Bernstein polynomial we can use the two diagonals of the triangle scheme to construct a division of the polynomial

$B(t) = \sum_{i=0}^n \beta_i^{(0)} b_{i,n}(t) \mbox{ , } \qquad t \in [0,1]$

into

$B_1(t) = \sum_{i=0}^n \beta_0^{(i)} b_{i,n}\left(\frac{t}{t_0}\right) \mbox{ , } \qquad t \in [0,t_0]$

and

$B_2(t) = \sum_{i=0}^n \beta_{n-i}^{(i)} b_{i,n}\left(\frac{t-t_0}{1-t_0}\right) \mbox{ , } \qquad t \in [t_0,1]$

Example

We want to evaluate the Bernstein polynomial of degree 2 with the Bernstein coefficients

$\beta_0^{(0)} = \beta_0$

$\beta_1^{(0)} = \beta_1$

$\beta_2^{(0)} = \beta_2$

at the point t₀.

We start the recursion with

$\beta_0^{(1)} = \beta_0^{(0)} (1-t_0) + \beta_1^{(0)}t_0 = \beta_0(1-t_0) + \beta_1 t_0$

$\beta_1^{(1)} = \beta_1^{(0)} (1-t_0) + \beta_2^{(0)}t_0 = \beta_1(1-t_0) + \beta_2 t_0$

and with the second iteration the recursion stops with

$\begin{align} \beta_0^{(2)} & = \beta_0^{(1)} (1-t_0) + \beta_1^{(1)} t_0 \\ \ & = \beta_0(1-t_0) (1-t_0) + \beta_1 t_0 (1-t_0) + \beta_1(1-t_0)t_0 + \beta_2 t_0 t_0 \\ \ & = \beta_0 (1-t_0)^2 + \beta_1 2t_0(1-t_0) + \beta_2 t_0^2 \end{align}$

which is the expected Bernstein polynomial of degree n.

Bézier curve

When evaluating a Bézier curve of degree n in 3 dimensional space with n+1 control points P_i

$\mathbf{B}(t) = \sum_{i=0}^{n} \mathbf{P}_i b_{i,n}(t) \mbox{ , } t \in [0,1]$

with

$\mathbf{P}_i := \begin{pmatrix} x_i \\ y_i \\ z_i \end{pmatrix}$.

we split the Bézier curve into three separate equations

$B_1(t) = \sum_{i=0}^{n} x_i b_{i,n}(t) \mbox{ , } t \in [0,1]$

$B_2(t) = \sum_{i=0}^{n} y_i b_{i,n}(t) \mbox{ , } t \in [0,1]$

$B_3(t) = \sum_{i=0}^{n} z_i b_{i,n}(t) \mbox{ , } t \in [0,1]$

which we evaluate individually using De Casteljau's algorithm.

Geometric interpretation

The geometric interpretation of De Casteljau's algorithm is straightforward.

• Consider a Bézier curve with control points $\scriptstyle P_0,...,P_n$. Connecting the consecutive points we create the control polygon of the curve.
• Subdivide now each line segment of this polygon with the ratio $\scriptstyle t : (1-t)$ and connect the points you get. This way you arrive at the new polygon having one less segment.
• Repeat the process till you arrive at the single point - this is the point of the curve corresponding to the parameter $\scriptstyle t$.

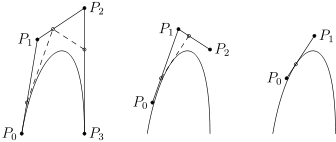
The following picture shows this process for a cubic Bézier curve:

Note that the intermediate points that were constructed are in fact the control points for two new Bezier curves, both exactly coincident with the old one. This algorithm not only evaluates the curve at $\scriptstyle t$, but splits the curve into two pieces at $\scriptstyle t$, and provides the equations of the two sub-curves in Bezier form.

The interpretation given above is valid for a nonrational Bezier curve. To evaluate a rational Bezier curve in $\scriptstyle \mathbf{R}^n$, we may project the point into $\scriptstyle \mathbf{R}^{n+1}$; for example, a curve in three dimensions may have its control points $\scriptstyle \{(x_i, y_i, z_i)\}$ and weights $\scriptstyle \{w_i\}$ projected to the weighted control points $\scriptstyle \{(w_ix_i, w_iy_i, w_iz_i, w_i)\}$. The algorithm then proceeds as usual, interpolating in $\scriptstyle \mathbf{R}^4$. The resulting four-dimensional points may be projected back into three-space with a perspective divide.

In general, operations on a rational curve (or surface) are equivalent to operations on a nonrational curve in a projective space. This representation as the "weighted control points" and weights is often convenient when evaluating rational curves.

References

• Farin, Gerald & Hansford, Dianne (2000). The Essentials of CAGD. Natic, MA: A K Peters, Ltd. ISBN 1-56881-123-3

See also

• Bézier curves
• De Boor's algorithm
• Horner scheme to evaluate polynomials in monomial form
• Clenshaw algorithm to evaluate polynomials in Chebyshev form