Doomsday rule

John Conway, inventor of the Doomsday algorithm

The Doomsday rule or Doomsday algorithm is a way of calculating the day of the week of a given date. It provides a perpetual calendar since the Gregorian calendar moves in cycles of 400 years.

This algorithm for mental calculation was devised by John Conway ^[1][2] after drawing inspiration from Lewis Carroll's work on a perpetual calendar algorithm.^[3][4] It takes advantage of the fact that each year has a certain day of the week (the doomsday) upon which certain easy-to-remember dates fall; for example, 4/4, 6/6, 8/8, 10/10, 12/12, and the last day of February all occur on the same day of the week in any given year. Applying the Doomsday algorithm involves three steps:

1. Determine the "anchor day" for the century.
2. Use the anchor day for the century to calculate the doomsday for the year.
3. Choose the closest date out of the ones that always fall on the doomsday (e.g. 4/4, 6/6, 8/8), and count the number of days (mod 7) between that date and the date in question to arrive at the day of the week.

This technique applies to both the Gregorian calendar A.D. and the Julian calendar, although their doomsdays will usually be different days of the week.

Since this algorithm involves treating days of the week like numbers mod 7, John Conway suggests thinking of the days of the week as Noneday, Oneday, Twosday, Treblesday, Foursday, Fiveday, and Six-a-day.

The algorithm is simple enough for anyone with basic arithmetic ability to do the calculations mentally. Conway can usually give the correct answer in under two seconds. To improve his speed, he practices his calendrical calculations on his computer, which is programmed to quiz him with random dates every time he logs on. ^[5]

Doomsdays for some contemporary years

Doomsday for the current year (2011) is Monday.

For some other contemporary years:

2004	Sunday
2005	Monday
2006	Tuesday
2007	Wednesday
2008	Friday
2009	Saturday
2010	Sunday
2011	Monday
2012	Wednesday
2013	Thursday
2014	Friday
2015	Saturday
2016	Monday

Memorable dates that always land on Doomsday

One can easily find the day of the week of a given calendar date by using a nearby Doomsday as a reference point. To help with this, the following is a list of easy-to-remember dates for each month that always land on the doomsday.

As mentioned above, the last day of February always falls on the doomsday, as do the double dates 4/4, 6/6, 8/8, 10/10, and 12/12. Four of the odd month dates (5/9, 9/5, 7/11, and 11/7) can be remembered with the mnemonic "I work from 9 to 5 at the 7-11." For March, one can remember the pseudo-date "March 0", which refers to the day before 3/1, i.e. the last day of February; one can alternately remember the date a week later, 3/7, or 3/21 which is often the first day of spring in the northern hemisphere. For January, 1/11 is a doomsday during leap years, while 1/10 is a doomsday during common years; 1/3 is a doomsday during common years and 1/4 a doomsday during leap years, which can be remembered as "the 3rd during 3 years in 4, and the 4th in the 4th".

Month	Memorable date	Mnemonic
January	1/3 (common years), 1/4 (leap years) 1/10 (common years), 1/11 (leap years)	the 3rd 3 years in 4 and the 4th in the 4th all ones
February	2/28 (common years), 2/29 (leap years)	last day of February
March	"3/0", 3/7 3/21	last day of February often first day of spring
April	4/4	even month
May	5/9	9-to-5 at 7-11
June	6/6	even month
July	7/11	9-to-5 at 7-11
August	8/8	even month
September	9/5	9-to-5 at 7-11
October	10/10	even month
November	11/7	9-to-5 at 7-11
December	12/12	even month

Since the Doomsday for a particular year is directly related to weekdays of dates in the period from March through February of the next year, common years and leap years have to be distinguished for January and February of the same year.

Examples

Suppose you want to know which day of the week Christmas Day of 2006 was. In the year 2006, Doomsday was Tuesday. Since December 12 is a Doomsday, December 25, being thirteen days afterwards (two weeks less a day), fell on a Monday.

It's useful to note that Christmas Day is always the day before Doomsday ("One off Doomsday"). In addition, July 4 is always on a Doomsday, and so is Halloween.

Suppose that you want to find the day of week that the September 11, 2001 attacks on the World Trade Center occurred. The century anchor was Tuesday, and Doomsday for 2001 is one day beyond, which is Wednesday. September 5 was a Doomsday, and September 11, six days later, fell on a Tuesday.

Finding a year's Doomsday

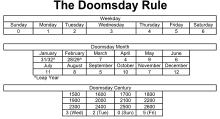
We first take the anchor day for the century. For the purposes of the Doomsday rule, a century starts with a 00 year and ends with a 99 year. The following table shows the anchor day of centuries 1800–1899, 1900–1999, 2000–2099 and 2100–2199.

Century	Anchor day	Mnemonic	Index (day of week)
1800–1899	Friday	-	5 (Fiveday)
1900–1999	Wednesday	We-in-dis-day (most living people were born in that century)	3 (Treblesday)
2000–2099	Tuesday	Y-Tue-K or Twos-day (Y2K was at the head of this century)	2 (Twosday)
2100–2199	Sunday	Twenty-one-day is Sunday (2100 is the start of the next century)	0 (Noneday)

Next, we find the year's Doomsday. To accomplish that according to Conway:

1. Divide the year's last two digits (call this y) by 12 and let a be the floor of the quotient.
2. Let b be the remainder of the same quotient.
3. Divide that remainder by 4 and let c be the floor of the quotient.
4. Let d be the sum of the three numbers (d = a + b + c). (It is again possible here to divide by seven and take the remainder. This number is equivalent, as it must be, to the sum of the last two digits of the year taken collectively plus the floor of those collective digits divided by four.)
5. Count forward the specified number of days (d or the remainder of d/7) from the anchor day to get the year's Doomsday.

$\begin{matrix}\left({\left\lfloor{\frac{y}{12}}\right\rfloor+y \bmod 12+\left\lfloor{\frac{y \bmod 12}{4}}\right\rfloor}\right) \bmod 7+\rm{anchor}=\rm{Doomsday}\end{matrix}$

For the twentieth-century year 1966, for example:

$\begin{matrix}\left({\left\lfloor{\frac{66}{12}}\right\rfloor+66 \bmod 12+\left\lfloor{\frac{66 \bmod 12}{4}}\right\rfloor}\right) \bmod 7+\rm{Wednesday} & = & \left(5+6+1\right) \bmod 7+\rm{Wednesday} \\ \ & = & \rm{Monday}\end{matrix}$

As described in bullet 4, above, this is equivalent to:

$\begin{matrix}\left({66 + \left\lfloor{\frac{66}{4}}\right\rfloor}\right) \bmod 7+\rm{Wednesday} & = & \left(66+16\right) \bmod 7+\rm{Wednesday} \\ \ & = & \rm{Monday}\end{matrix}$

So Doomsday in 1966 fell on Monday.

Similarly, Doomsday in 2005 is on a Monday:

$\left({\left\lfloor{\frac{5}{12}}\right\rfloor+5 \bmod 12+\left\lfloor{\frac{5 \bmod 12}{4}}\right\rfloor}\right) \bmod 7+\rm{Tuesday}=\rm{Monday}$

Why it works

Doomsday rule

The doomsday calculation is effectively calculating the number of days between any given date in the base year and the same date in the current year, then taking the remainder modulo 7. When both dates come after the leap day (if any), the difference is just 365y plus y/4 (rounded down). But 365 equals 52*7+1, so after taking the remainder we get just

$(y + \lfloor \frac{y}{4} \rfloor) \bmod 7.$

This gives a simpler formula if one is comfortable dividing large values of y by both 4 and 7. For example, we can compute $(66 + \lfloor \frac{66}{4} \rfloor) \bmod 7 = (66 + 16) \bmod 7 = 82 \bmod 7 = 5$, which gives the same answer as in the example above.

Where 12 comes in is that the pattern of $(y + \lfloor \frac{y}{4} \rfloor) \bmod 7$ almost repeats every 12 years. After 12 years, we get (12 + 12/4) mod 7 = 15 mod 7 = 1. If we replace y by y mod 12, we are throwing this extra day away; but adding back in $\lfloor \frac{y}{12} \rfloor$ compensates for this error, giving the final formula.

The Odd+11 method

A simpler method for finding the year's doomsday was discovered in 2010. Called the Odd+11 method, it has been proved^[6] equivalent to computing

$(y + \lfloor \frac{y}{4} \rfloor) \, \operatorname{mod} \, 7.$

It is well suited to mental calculation, because it requires no division by 4 (or 12), and the procedure is easy to remember because of its repeated use of the "odd+11" rule.

The procedure accumulates a running total T as follows:

1. Let T be the year's last two digits.
2. If T is odd, add 11.
3. Let T = T/2.
4. If T is odd, add 11.
5. Let T = 7 − (T mod 7).
6. Count forward T days from the anchor day to get the year's Doomsday.

Applying this method to the year 1966, for example, the steps as outlined would be:

1. T = 66
2. T = 66 (Do nothing since T is even.)
3. T = 66/2 = 33
4. T = 33+11 = 44 (Add 11 because T is odd.)
5. T = 7 − (44 mod 7) = 7 − 2 = 5
6. Doomsday 1966 = 5 + Wednesday = Monday

Finding a century's anchor day

To find a century's anchor day, begin by finding the century c in which the date falls. (For the purposes of this calculation, century years are treated as though they fall in the century that follows. 2000 is therefore part of the 21st century in this equation, not the 20th century.) A year's century number is equal to its first two digits plus one. Take the century number and multiply by 5. Separately, subtract one from the century number, divide by four and take the floor of the quotient. Add these two numbers modulo 7 and use the result to offset from Thursday to get the anchor day.

$\left({5c+\left\lfloor{\frac{c-1}{4}}\right\rfloor}\right) \bmod 7+\rm{Thursday}=\rm{anchor}$

The anchor day for the twenty-first century is Tuesday:
$\left({5\times{21}+\left\lfloor{\frac{20}{4}}\right\rfloor}\right) \bmod 7+\rm{Thursday}=\rm{Tuesday}$

Overview of all Doomsdays

Month	Dates	Week numbers *
January (common years)	3, 10, 17, 24, 31	1–5
January (leap years)	4, 11, 18, 25	1–4
February (common years)	7, 14, 21, 28	6–9
February (leap years)	1, 8, 15, 22, 29	5–9
March	7, 14, 21, 28	10–13
April	4, 11, 18, 25	14–17
May	2, 9, 16, 23, 30	18–22
June	6, 13, 20, 27	23–26
July	4, 11, 18, 25	27–30
August	1, 8, 15, 22, 29	31–35
September	5, 12, 19, 26	36–39
October	3, 10, 17, 24, 31	40–44
November	7, 14, 21, 28	45–48
December	5, 12, 19, 26	49–52

* In leap years the nth Doomsday is in ISO week n. In common years the day after the nth Doomsday is in week n. Thus in a common year the week number on the Doomsday itself is one less if it is a Sunday, i.e., in a common year starting on Friday.

Computer formula for the Doomsday of a year

For computer use, the following formulas for the Doomsday of a year are convenient.

For the Gregorian calendar:

$\mbox{Doomsday} = \mbox{Tuesday} + y + \left\lfloor\frac{y}{4}\right\rfloor - \left\lfloor\frac{y}{100}\right\rfloor + \left\lfloor\frac{y}{400}\right\rfloor$

For example, the year 2009 has a doomsday of Saturday under the Gregorian calendar (the currently accepted calendar), since

$\mbox{Saturday (6)} \mod 7 = \mbox{Tuesday (2)} + 2009 + \left\lfloor\frac{2009}{4}\right\rfloor - \left\lfloor\frac{2009}{100}\right\rfloor + \left\lfloor\frac{2009}{400}\right\rfloor$

$= ( 2 + 2009 + 502 - 20 + 5) \mod 7 = (2 + 0 + 5 - 6 + 5) \mod 7 = 6$

For the Julian calendar:

$\mbox{Doomsday} = \mbox{Sunday} + y + \left\lfloor\frac{y}{4}\right\rfloor$

The formulas apply also for the proleptic Gregorian calendar and the proleptic Julian calendar. They use the floor function and astronomical year numbering for years BC.

For comparison, see the calculation of a Julian day number.

400-year cycle of Doomsdays

Since in the Gregorian calendar there are 146097 days, or exactly 20871 seven-day weeks, in 400 years, the anchor day repeats every four centuries. For example, the anchor day of 1700–1799 is the same as the anchor day of 2100–2199, i.e. Sunday.

The full 400-year cycle of Doomsdays is given in the following table. The centuries are for the Gregorian and proleptic Gregorian calendar, unless marked with a J for Julian (for the latter not all centuries are shown, for the missing ones it is easy to interpolate). The Gregorian leap years are highlighted.

	-200J 500J 1200J 1900J -400 00 400 800 1200 1600 2000	-00J 700J 1400J 2100J -300 100 500 900 1300 1700 2100	200J 900J 1600J 2300J -200 200 600 1000 1400 1800 2200	400J 1100J 1800J 2500J -100 300 700 1100 1500 1900 2300
00	Tu	Su	Fr	We
01 29 57 85	We	Mo	Sa	Th
02 30 58 86	Th	Tu	Su	Fr
03 31 59 87	Fr	We	Mo	Sa
04 32 60 88	Su	Fr	We	Mo
05 33 61 89	Mo	Sa	Th	Tu
06 34 62 90	Tu	Su	Fr	We
07 35 63 91	We	Mo	Sa	Th
08 36 64 92	Fr	We	Mo	Sa
09 37 65 93	Sa	Th	Tu	Su
10 38 66 94	Su	Fr	We	Mo
11 39 67 95	Mo	Sa	Th	Tu
12 40 68 96	We	Mo	Sa	Th
13 41 69 97	Th	Tu	Su	Fr
14 42 70 98	Fr	We	Mo	Sa
15 43 71 99	Sa	Th	Tu	Su
16 44 72	Mo	Sa	Th	Tu
17 45 73	Tu	Su	Fr	We
18 46 74	We	Mo	Sa	Th
19 47 75	Th	Tu	Su	Fr
20 48 76	Sa	Th	Tu	Su
21 49 77	Su	Fr	We	Mo
22 50 78	Mo	Sa	Th	Tu
23 51 79	Tu	Su	Fr	We
24 52 80	Th	Tu	Su	Fr
25 53 81	Fr	We	Mo	Sa
26 54 82	Sa	Th	Tu	Su
27 55 83	Su	Fr	We	Mo
28 56 84	Tu	Su	Fr	We
	2000 2400	2100 2500	2200 2600	2300 2700

Negative years use astronomical year numbering. Year 25BC is −24, shown in the column of −100J (proleptic Julian) or −100 (proleptic Gregorian), at the row 76.

Frequency in the 400-year cycle (leap years are widened again):

• 44 × Thursday, Saturday (non-leap years)
• 43 × Monday, Tuesday, Wednesday, Friday, Sunday (non-leap years)
• 15 × Monday, Wednesday (leap years)
• 14 × Friday, Saturday (leap years)
• 13 × Tuesday, Thursday, Sunday (leap years)

Adding common and leap years:

• 58 × Monday, Wednesday, Saturday
• 57 × Thursday, Friday
• 56 × Tuesday, Sunday

A leap year with Monday as Doomsday means that Sunday is one of 97 days skipped in the 497-day sequence. Thus the total number of years with Sunday as Doomsday is 71 minus the number of leap years with Monday as Doomsday, etc. Since Monday as Doomsday is skipped across 29 February 2000 and the pattern of leap days is symmetric about that leap day, the frequencies of Doomsdays per weekday (adding common and leap years) are symmetric about Monday. The frequencies of Doomsdays of leap years per weekday are symmetric about the Doomsday of 2000, Tuesday.

The frequency of a particular date being on a particular weekday can easily be derived from the above (for a date from 1 January - 28 February, relate it to the Doomsday of the previous year).

For example, 28 February is one day after Doomsday of the previous year, so it is 58 times each on Tuesday, Thursday and Sunday, etc. 29 February is Doomsday of a leap year, so it is 15 times each on Monday and Wednesday, etc.

28-year cycle

Regarding the frequency of Doomsdays in a Julian 28-year cycle, there are 1 leap year and 3 common years for every weekday, the latter 6, 17 and 23 years after the former (so with intervals of 6, 11, 6, and 5 years; not evenly distributed because after 12 years the day is skipped in the sequence of Doomsdays).^{[citation needed]} The same cycle applies for any given date from 1 March falling on a particular weekday.

For any given date up to 28 February falling on a particular weekday, the 3 common years are 5, 11, and 22 years after the leap year, so with intervals of 5, 6, 11, and 6 years. Thus the cycle is the same, but with the 5-year interval after instead of before the leap year.

Thus, for any date except 29 February, the intervals between common years falling on a particular weekday are 6, 11, 11. See e.g. at the bottom of the page Common year starting on Monday the years in the range 1906–2091.

For 29 February falling on a particular weekday, there is just one in every 28 years, and it is of course a leap year.

Julian calendar

The Gregorian calendar accurately lines up with astronomical events such as solstices. In 1582 this modification of the Julian calendar was first instituted. In order to correct for calendar drift, 10 days were skipped, so Doomsday moved back 10 days (i.e. 3 days): Thursday 4 October (Julian, Doomsday is Wednesday) was followed by Friday 15 October (Gregorian, Doomsday is Sunday). The table includes Julian calendar years, but the algorithm is for the Gregorian and proleptic Gregorian calendar only.

Note that the Gregorian calendar was not adopted simultaneously in all countries, so for many centuries, different regions used different dates for the same day.

Correspondence with dominical letter

Doomsday is related to the dominical letter of the year as follows.

Dominical letter	Doomsday
A or BA	Tuesday
B or CB	Monday
C or DC	Sunday
D or ED	Saturday
E or FE	Friday
F or GF	Thursday
G or AG	Wednesday

Full examples

Example 1 (1985)

Suppose you want to know the day of the week of September 18, 1985. You begin with the century day, Wednesday. To this, we'll add three things, called a, b, and c above:

• a is the floor of 85/12, which is 7.
• b is 85 mod 12, which is 1.
• c is the floor of b/4, which is 0.

This yields 8, which is equivalent to 1 mod 7. Thus, Doomsday in 1985 was a Thursday. We now compare September 18 to a nearby Doomsday. Since September 5 is a Doomsday, we see that the 18th is 13 past a Doomsday, which is equivalent to −1 mod 7. Thus, we take one away from Thursday to find that September 18, 1985 was a Wednesday.

Example 2 (other centuries)

Suppose that you want to find the day of week that the American Civil War broke out at Fort Sumter, which was April 12, 1861. The anchor day for the century was 99 days after Thursday, or, in other words, Friday (calculated as (18+1)*5+floor(18/4); or just look at the chart, above, which lists the century's anchor days). The digits 61 gave a displacement of six days so Doomsday was Thursday. Therefore, April 4 was Thursday so April 12, eight days later, was a Friday.

See also

Calendars:

• Mon - Tue - Wed - Thu - Fri - Sat - Sun – common years with the given Doomsday
• Mon - Tue - Wed - Thu - Fri - Sat - Sun – leap years with the given Doomsday
• Ordinal date
• Computus – Gauss algorithm for Easter date calculation
• Zeller's congruence - An algorithm (1882) to calculate the day of the week for any Julian or Gregorian calendar date.
• mental calculation

References

1. ^ John Horton Conway, "Tomorrow is the Day After Doomsday", Eureka, volume 36, pages 28-31, October 1973.
2. ^ Richard Guy, John Horton Conway, Elwyn Berlekamp : "Winning Ways: For Your Mathematical Plays, Volume. 2: Games in Particular", pages 795-797, Academic Press, London, 1982, ISBN 01-12-091102-7.
3. ^ Lewis Carroll, "To Find the Day of the Week for Any Given Date", Nature, March 31, 1887.
4. ^ Martin Gardner, "The Universe in a Handkerchief: Lewis Carroll's Mathematical Recreations, Games, Puzzles, and Word Plays", pages 24-26, Springer-Verlag, 1996
5. ^ Alpert, Mark. "Not Just Fun and Games", Scientific American, April, 1999.
6. ^ Chamberlain Fong, Michael K. Walters: "Methods for Accelerating Conway's Doomsday Algorithm (part 2)", 7th International Congress of Industrial and Applied Mathematics (2011).

External links

• COWAFOGO • Weekday Solving Simplified, 2011
• Encyclopedia of Weekday Calculation by Hans-Christian Solka, 2010
• Doomsday calculator that also "shows all work"
• World records for mentally calculating the day of the week in the Gregorian Calendar
• What is the day of the week, given any date?
• Doomsday Algorithm
• Finding the Day of the Week
• Poem explaining the Doomsday rule at the Wayback Machine (archived October 18, 2006)