Descartes' theorem

For other uses, see Descartes' theorem (disambiguation).

In geometry, Descartes' theorem, named after René Descartes, establishes a relationship between four kissing, or mutually tangent, circles. The theorem can be used to construct a fourth circle tangent to three given, mutually tangent circles.

History

Geometrical problems involving tangent circles have been pondered for millennia. In ancient Greece of the third century BC, Apollonius of Perga devoted an entire book to the topic. Unfortunately the book, which was called On Tangencies, is not among his surviving works.

René Descartes discussed the problem briefly in 1643, in a letter to Princess Elizabeth of Bohemia. He came up with essentially the same solution as given in equation (1) below, and thus attached his name to the theorem.

Frederick Soddy rediscovered the equation in 1936. The kissing circles in this problem are sometimes known as Soddy circles, perhaps because Soddy chose to publish his version of the theorem in the form of a poem titled The Kiss Precise, which was printed in Nature (June 20, 1936). Soddy also extended the theorem to spheres; Thorold Gosset extended the theorem to arbitrary dimensions.

Definition of curvature

Kissing circles. Given three mutually tangent circles (black), what radius can a fourth tangent circle have? There are in general two possible answers (red).

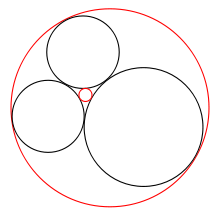
Descartes' theorem is most easily stated in terms of the circles' curvatures. The curvature (or bend) of a circle is defined as k = ±1/r, where r is its radius. The larger a circle, the smaller is the magnitude of its curvature, and vice versa.

The plus sign in k = ±1/r applies to a circle that is externally tangent to the other circles, like the three black circles in the image. For an internally tangent circle like the big red circle, that circumscribes the other circles, the minus sign applies.

If a straight line is considered a degenerate circle with zero curvature (and thus infinite radius), Descartes' theorem also applies to a line and two circles that are all three mutually tangent, giving the radius of a third circle tangent to the other two circles and the line.

Descartes' theorem

If four circles are tangent to each other at six distinct points, and the circles have curvatures k_i (for i = 1, ..., 4), Descartes' theorem says:

(1)

$(k_1+k_2+k_3+k_4)^2=2\,(k_1^2+k_2^2+k_3^2+k_4^2).$

When trying to find the radius of a fourth circle tangent to three given kissing circles, the equation is best rewritten as:

(2)

$k_4 = k_1 + k_2 + k_3 \pm2 \sqrt{k_1 k_2 + k_2 k_3 + k_3 k_1}. \,$

The ± sign reflects the fact that there are in general two solutions. Ignoring the degenerate case of a straight line, one solution is positive and the other is either positive or negative; if negative, it represents a circle that circumscribes the first three (as shown in the diagram above).

Other criteria may favor one solution over the other in any given problem.

Special cases

One of the circles is replaced by a straight line of zero curvature. Descartes' theorem still applies.

Here, as all three circles are tangent to each other at the same point, Descartes' theorem does not apply.

If one of the three circles is replaced by a straight line, then one k_i, say k₃, is zero and drops out of equation (1). Equation (2) then becomes much simpler:

(3)

$k_4=k_1+k_2\pm2\sqrt{k_1k_2}.$

If two circles are replaced by lines, the tangency between the two replaced circles becomes a parallelism between their two replacement lines. For all four curves to remain mutually tangent, the other two circles must be congruent. In this case, with k₂ = k₃ = 0, equation (2) is reduced to the trivial

$\displaystyle k_4=k_1.$

It is not possible to replace three circles by lines, as it is not possible for three lines and one circle to be mutually tangent. Descartes' theorem does not apply when all four circles are tangent to each other at the same point.

Another special case is when the k_i are squares,

$(v^2+x^2+y^2+z^2)^2=2\,(v^4+x^4+y^4+z^4)$

Euler showed that this is equivalent to the simultaneous triplet of Pythagorean triples,

$(2vx)^2+(2yz)^2 =\, (v^2+x^2-y^2-z^2)^2$

$(2vy)^2+(2xz)^2 =\, (v^2-x^2+y^2-z^2)^2$

$(2vz)^2+(2xy)^2 =\, (v^2-x^2-y^2+z^2)^2$

and can be given a parametric solution. When the minus sign of a curvature is chosen,

$(-v^2+x^2+y^2+z^2)^2=2\,(v^4+x^4+y^4+z^4)$

this can be solved^[1] as,

$[v, x, y, z] =\, [2(ab-cd)(ab+cd), (a^2+b^2+c^2+d^2)(a^2-b^2+c^2-d^2), 2(ac-bd)(a^2+c^2), 2(ac-bd)(b^2+d^2)]$

where,

$a^4+b^4 =\, c^4+d^4$

parametric solutions of which are well-known.

Complex Descartes theorem

To determine a circle completely, not only its radius (or curvature), but also its center must be known. The relevant equation is expressed most clearly if the coordinates (x, y) are interpreted as a complex number z = x + iy. The equation then looks similar to Descartes' theorem and is therefore called the complex Descartes theorem.

Given four circles with curvatures k_i and centers z_i (for i = 1...4), the following equality holds in addition to equation (1):

(4)

$(k_1z_1+k_2z_2+k_3z_3+k_4z_4)^2=2\,(k_1^2z_1^2+k_2^2z_2^2+k_3^2z_3^2+k_4^2z_4^2).$

Once k₄ has been found using equation (2), one may proceed to calculate z₄ by rewriting equation (4) to a form similar to equation (2):

$z_4 = \frac{z_1 k_1 + z_2 k_2 + z_3 k_3 \pm 2 \sqrt{k_1 k_2 z_1 z_2 + k_2 k_3 z_2 z_3 + k_1 k_3 z_1 z_3} }{k_4}.$

Again, in general, there are two solutions for z₄, corresponding to the two solutions for k₄.

Generalizations

The generalization to n dimensions is sometimes referred to as the Soddy–Gosset theorem, even though it was shown by R. Lachlan in 1886. In n-dimensional Euclidean space, the maximum number of mutually tangent (n − 1)-spheres is n + 2. For example, in 3-dimensional space, five spheres can be mutually tangent.The curvatures of the hyperspheres satisfy

$\left(\sum_{i=1}^{n+2} k_i\right)^2 = n\,\sum_{i=1}^{n+2} k_i^2$

with the case k_i = 0 corresponding to a flat hyperplane, in exact analogy to the 2-dimensional version of the theorem.

Although there is no 3-dimensional analogue of the complex numbers, the relationship between the positions of the centers can be re-expressed as a matrix equation, which also generalizes to n dimensions.^[2]

See also

• Ford circles
• Apollonian gasket
• Soddy's hexlet
• Tangent lines to circles

Notes

1. ^ A Collection of Algebraic Identities: Sums of Three or More 4th Powers
2. ^ Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks (April 2002). "Beyond the Descartes Circle Theorem". The American Mathematical Monthly 109 (4): 338–361. JSTOR 2695498. 

External links

• An interactive Apollonian gasket using Descartes' theorem running on pure HTML5
• Interactive applet demonstrating four mutually tangent circles at cut-the-knot
• The Kiss Precise
• XScreenSaver: Screenshots :: An XScreenSaver display hack visualizes Descartes’ theorem, in hack “Apollonian”.
• Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks: Beyond The Descartes Circle Theorem