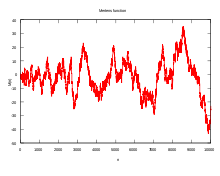
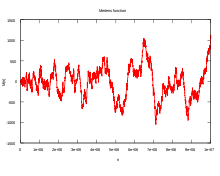
Mertens function

Mertens function to n=10,000

Mertens function to n=10,000,000

In number theory, the Mertens function is defined for all positive integers n as

$M(n) = \sum_{k=1}^n \mu(k)$

where μ(k) is the Möbius function. The function is named in honour of Franz Mertens.

Less formally, M(n) is the count of square-free integers up to n that have an even number of prime factors, minus the count of those that have an odd number. The Mertens function slowly grows in positive and negative directions both on average and in peak value, oscillating in an apparently chaotic manner passing through zero when n has the values

2, 39, 40, 58, 65, 93, 101, 145, 149, 150, 159, 160, 163, 164, 166, 214, 231, 232, 235, 236, 238, 254, ... (sequence A028442 in OEIS).

Because the Möbius function only takes the values −1, 0, and +1, the Mertens function moves slowly and there is no n such that |M(n)| > n. The Mertens conjecture went further, stating that there would be no n where the absolute value of the Mertens function exceeds the square root of n. The Mertens conjecture was proven false in 1985 by Andrew Odlyzko and Herman te Riele. However, the Riemann hypothesis is equivalent to a weaker conjecture on the growth of M(n), namely M(n) = O(n^{1/2 + ε}). Since high values for M(n) grow at least as fast as the square root of n, this puts a rather tight bound on its rate of growth. Here, O refers to Big O notation.

The above definition can be extended to real numbers as follows:

$M(x) = \sum_{1\le k \le x} \mu(k).$

Representations

As an integral

Using the Euler product one finds that

$\frac{1}{\zeta(s) }= \prod_{p} (1-p^{-s})= \sum_{n=1}^{\infty} \frac{\mu(n)}{n^s}$

where ζ(s) is the Riemann zeta function and the product is taken over primes. Then, using this Dirichlet series with Perron's formula, one obtains:

$\frac{1}{2\pi i}\oint_{C} \frac{x^{s}}{s\zeta(s)} \, ds = M(x)$

where C is a closed curve^{[disambiguation needed ]} encircling all of the roots of ζ(s).

Conversely, one has the Mellin transform

$\frac{1}{\zeta(s)} = s\int_1^\infty \frac{M(x)}{x^{s+1}}\,dx$

which holds for Re(s) > 1.

A curious relation given by Mertens himself involving the second Chebyshev function is

$\Psi (x) = M\left( \frac{x}{2} \right) \log(2)+M \left( \frac{x}{3} \right) \log(3) + M \left( \frac{x}{4}\right )\log(4) + \cdots.$

A good evaluation, at least asymptotically, would be to obtain, by the method of steepest descent, the inequality

$\oint_C F(s)e^{st} \, ds \sim M(e^{t}).$

Assuming that there are not multiple non-trivial roots of ζ(ρ) we have the "exact formula" by the residue theorem:

$\frac{1}{2 \pi i} \oint_C \frac{x^s}{s \zeta (s)} \, ds = \sum_\rho \frac{x^\rho}{\rho \zeta'(\rho)} - 2+\sum_{n=1}^\infty \frac{ (-1)^{n-1} (2\pi )^{2n}}{(2n)! n \zeta(2n+1)x^{2n}}.$

Weyl conjectured that the Mertens function satisfied the approximate functional-differential equation

$\frac{y(x)}{2}-\sum_{r=1}^N \frac{B_{2r}}{(2r)!}D_t^{2r-1} y \left(\frac{x}{t+1}\right) + x\int_0^x \frac{y(u)}{u^{2}} \, du = x^{-1}H(\log x)$

where H(x) is the Heaviside step function, B are Bernoulli numbers and all derivatives with respect to t are evaluated at t = 0.

Titchmarsh (1960) provided a Trace formula involving a sum over the Möbius function and zeros of Riemann Zeta in the form

$\sum_{n=1}^{\infty}\frac{\mu(n)}{\sqrt{n}} g \log n = \sum_t \frac{h(t)}{\zeta'(1/2+it)}+2\sum_{n=1}^\infty \frac{ (-1)^{n} (2\pi )^{2n}}{(2n)! \zeta(2n+1)}\int_{-\infty}^{\infty}g(x) e^{-x(2n+1/2)} \, dx,$

where 't' sums over the imaginary parts of nontrivial zeros, and (g, h) are related by a Fourier transform, such that

$\pi g(x)= \int_{0}^{\infty}h(u)\cos(ux) \, du.$

As a sum over Farey sequences

Another formula for the Mertens function is

$M(n)= \sum_{a\in \mathcal{F}_n} e^{2\pi i a}$   where   $\mathcal{F}_n$   is the Farey sequence of order n.

This formula is used in the proof of the Franel–Landau theorem.^[1]

As a determinant

M(n) is the determinant of the n × n Redheffer matrix, a (0,1) matrix in which a_ij is 1 if either j is 1 or i divides j.

Calculation

The Mertens function has been computed for an increasing range of n.

Person	Year	Limit
Mertens	1897	104
von Sterneck	1897	1.5×105
von Sterneck	1901	5×105
von Sterneck	1912	5×106
Neubauer	1963	108
Cohen and Dress	1979	7.8×109
Dress	1993	1012
Lioen and van de Lune	1994	1013
Kotnik and van de Lune	2003	1014

Notes

1. ^ Edwards, Ch. 12.2

References

• Edwards, Harold (1974). Riemann's Zeta Function. Mineola, New York: Dover. ISBN 0-486-41740-9. 
• F. Mertens, "Über eine zahlentheoretische Funktion", Akademie Wissenschaftlicher Wien Mathematik-Naturlich Kleine Sitzungsber, IIa 106, (1897) 761–830.
• A. M. Odlyzko and Herman te Riele, "Disproof of the Mertens Conjecture", Journal für die reine und angewandte Mathematik 357, (1985) pp. 138–160.
• Weisstein, Eric W., "Mertens function" from MathWorld.
• Values of the Mertens function for the first 10,000 n are given by  A002321.
• Deléglise, M. and Rivat, J. "Computing the Summation of the Möbius Function." Experiment. Math. 5, 291-295, 1996. http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdf_1&handle=euclid.em/1047565447

External links

• Selected values of the Mertens function