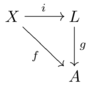Free Lie algebra

In mathematics, a free Lie algebra, over a given field K, is a Lie algebra generated by a set X, without any imposed relations.

Definition

Let X be a set and i: X → L a morphism of sets from X into a Lie algebra L. The Lie algebra L is called free on X if for any Lie algebra A with a morphism of sets f: X → A, there is a unique Lie algebra morphism g: L → A such that f = g o i.

Given a set X, one can show that there exists a unique free Lie algebra L(X) generated by X.

In the language of category theory, the functor sending a set X to the Lie algebra generated by X is the free functor from the category of sets to the category of Lie algebras. That is, it is left adjoint to the forgetful functor.

As the 0-graded component of the free Lie algebra on a set X is just the free vector space on that group, one can alternatively define a free Lie algebra on a vector space V as left adjoint to the forgetful functor from Lie algebras over a field K to vector spaces over the field K – forgetting the Lie algebra structure, but remembering the vector space structure.

Universal enveloping algebra

The universal enveloping algebra of a free Lie algebra on a set X is the free associative algebra generated by X. By the Poincaré-Birkhoff-Witt theorem it is the "same size" as the symmetric algebra of the free Lie algebra (meaning that if both sides are graded by giving elements of X degree 1 then they are isomorphic as graded vector spaces). This can be used to describe the dimension of the piece of the free Lie algebra of any given degree.

Witt showed that the number of basic commutators of degree k in the free Lie algebra on an m-element set is given by the necklace polynomial:

$N_k = \frac{1}{k}\sum_{d|k}\mu(d)\cdot m^{k/d},$

where μ is the Möbius function.

The graded dual of the universal enveloping algebra of a free Lie algebra on a finite set is the shuffle algebra.

Hall sets

An explicit basis of the free Lie algebra can be given in terms of a Hall set, which is a particular kind of subset inside the free magma on X. Elements of the free magma are binary trees, with their leaves labelled by elements of X. Hall sets were introduced by Marshall Hall (1950) based on work of Philip Hall on groups. Subsequently Wilhelm Magnus showed that they arise as the graded Lie algebra associated with the filtration on a free group given by the lower central series. This correspondence was motivated by commutator identities in group theory due to Philip Hall and Ernst Witt.

Lyndon basis

In particular there is a basis of the free Lie algebra corresponding to Lyndon words, called the Lyndon basis. (This is also called the Chen–Fox–Lyndon basis or the Lyndon–Shirshov basis, and is essentially the same as the Shirshov basis.) There is a bijection γ from the Lyndon words in an ordered alphabet to a basis of the free Lie algebra on this alphabet defined as follows.

• If a word w has length 1 then γ(w)=w (considered as a generator of the free Lie algebra).
• If w has length at least 2, then write w=uv for Lyndon words u, v with v as long as possible. Then γ(w) = [γ(u),γ(v)]

Shirshov–Witt theorem

Širšov (1953) and Witt (1956) showed that any Lie subalgebra of a free Lie algebra is itself a free Lie algebra.

Applications

The Milnor invariants of the link group are related to the free Lie algebra, as discussed in that article.

See also

• Free object
• Free algebra
• Free group

References

• Bakhturin, Yu.A. (2001), "Free Lie algebra over a ring", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/l/l058410.htm 
• N. Bourbaki, "Lie Groups and Lie Algebras," Chapter II: Free Lie Algebras, Springer, 1989. ISBN 0-387-50218-1
• Hall, Marshall (1950), "A basis for free Lie rings and higher commutators in free groups", Proceedings of the American Mathematical Society 1 (5): 575–581, doi:10.1090/S0002-9939-1950-0038336-7, ISSN 0002-9939, MR0038336, http://www.ams.org/journals/proc/1950-001-05/S0002-9939-1950-0038336-7/ 
• Chen, Kuo-Tsai; Fox, Ralph H.; Lyndon, Roger C. (1958), "Free differential calculus. IV. The quotient groups of the lower central series", Annals of Mathematics. Second Series 68 (1): 81–95, doi:10.2307/1970044, ISSN 0003-486X, JSTOR 1970044, MR0102539 
• Magnus, Wilhelm (1937), "Über Beziehungen zwischen höheren Kommutatoren" (in German), Journal für Reine und Angewandte Mathematik 177 (177): 105–115, doi:10.1515/crll.1937.177.105, ISSN 0075-4102, JFM 63.0065.01, http://resolver.sub.uni-goettingen.de/purl?GDZPPN00217412X 
• W. Magnus, A. Karrass, D. Solitar, "Combinatorial group theory". Reprint of the 1976 second edition, Dover, 2004. ISBN 0-486-43830-9
• G. Melançon (2001), "Hall set", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/h/h110040.htm 
• G. Melançon (2001), "Hall word", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/h/h110050.htm 
• Melançon, G. (2001), "Shirshov basis", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de//S/s110100.htm 
• Reutenauer, Christophe (1993), Free Lie algebras, London Mathematical Society Monographs. New Series, 7, The Clarendon Press Oxford University Press, ISBN 978-0-19-853679-6, MR1231799, http://books.google.com/books?id=cBvvAAAAMAAJ 
• Širšov, A. I. (1953), "Subalgebras of free Lie algebras", Mat. Sbornik N.S. 33(75): 441–452, MR0059892 
• Witt, Ernst (1956), "Die Unterringe der freien Lieschen Ringe", Mathematische Zeitschrift 64: 195–216, doi:10.1007/BF01166568, ISSN 0025-5874, MR0077525