Dürer graph

Dürer graph
Melencolia I by Albrecht Dürer, the first appearance of Dürer's solid (1514).

In the mathematical field of graph theory, the Dürer graph is an undirected graph with 12 vertices and 18 edges. It is named after Albrecht Dürer, whose 1514 engraving Melencolia I includes a depiction of Dürer's solid, a convex polyhedron having the Dürer graph as its skeleton. Dürer's solid is one of only four well-covered simple convex polyhedra.

Contents

Dürer's solid

Dürer's solid is combinatorially equivalent to a cube with two opposite vertices truncated,[1] although Dürer's depiction of it is not in this form but rather as a truncated rhombohedron.[2] The exact geometry of the solid depicted by Dürer is a subject of some academic debate.[3] Richter (1957) claims that the rhombi of the rhombohedron from which this shape is formed have 5:6 as the ratio between their short and long diagonals, from which the acute angles of the rhombi would be approximately 80°. Schröder (1980) and Lynch (1982) instead conclude that the ratio is √3:2 and that the angle is approximately 82°. MacGillavry (1981) measures features of the drawing and finds that the angle is approximately 79°. Schrieber (1999) argues based on the writings of Dürer that all vertices of Dürer's solid lie on a common sphere, and further claims that the rhombus angles are 72°. Weitzel (2004) analyzes a 1510 sketch by Dürer of the same solid, from which he confirms Schrieber's hypothesis that the shape has a circumsphere but with rhombus angles of approximately 79.5°.

Graph-theoretic properties

Dürer graph
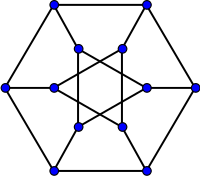
Dürer graph.svg
The Dürer graph
Named after Albrecht Dürer
Vertices 12
Edges 18
Diameter 4
Girth 3
Automorphisms 12 (D6)
Chromatic number 3
Chromatic index 3
Properties Cubic
Planar
well-covered
v · cubic graph of girth 3 and diameter 4. As well as its construction as the skeleton of Dürer's solid, it can be obtained by applying a Y-Δ transform to the opposite vertices of a cube graph, or as the generalized Petersen graph G(6,2). As with any graph of a convex polyhedron, the Dürer graph is a 3-vertex-connected simple planar graph.

The Dürer graph is a well-covered graph, meaning that all of its maximal independent sets have the same number of vertices, four. It is one of four well-covered cubic polyhedral graphs and one of seven well-covered 3-connected cubic graphs. The only other three well-covered simple convex polyhedra are the tetrahedron, triangular prism, and pentagonal prism.[4]

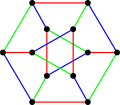
The Dürer graph is Hamiltonian, with LCF notation [-4,5,2,-4,-2,5;-].[5] More precisely, it has exactly six Hamiltonian cycles, each pair of which may be mapped into each other by a symmetry of the graph.[6]

Symmetries

The automorphism group both of the Dürer graph and of the Dürer solid (in either the truncated cube form or the form shown by Dürer) is isomorphic to the dihedral group of order 12 : D6.

Gallery

  • The chromatic index of the Dürer graph is 3.

  • The chromatic number of the Dürer graph is 3.

  • The Dürer graph is Hamiltonian.

Notes

  1. ^ Weisstein, Eric W., "Dürer's Solid" from MathWorld.
  2. ^ Weber (1900). According to Lynch (1982), the contrary hypothesis that the shape is a misdrawn truncated cube was promoted by Strauss (1972).
  3. ^ See Weitzel (2004), from which most of the following history is drawn.
  4. ^ Campbell & Plummer (1988); Campbell, Ellingham & Royce (1993).
  5. ^ Castagna and Prins attribute the proof of Hamiltonicity of a class of generalized Petersen graphs that includes the Dürer graph to a 1968 Ph.D. thesis of G. N. Robertson at the University of Waterloo. See Castagna, Frank; Prins, Geert (1972), "Every Generalized Petersen Graph has a Tait Coloring", Pacific Journal of Mathematics 40 .
  6. ^ Schwenk, Allen J. (1989), "Enumeration of Hamiltonian cycles in certain generalized Petersen graphs", Journal of Combinatorial Theory, Series B 47 (1): 53–59, doi:10.1016/0095-8956(89)90064-6, MR1007713 .

References

  • Campbell, S. R.; Ellingham, M. N.; Royle, Gordon F. (1993), "A characterisation of well-covered cubic graphs", Journal of Combinatorial Mathematics and Combinatorial Computing 13: 193–212, MR1220613 .
  • Campbell, Stephen R.; Plummer, Michael D. (1988), "On well-covered 3-polytopes", Ars Combinatoria 25 (A): 215–242, MR942505 .
  • Lynch, Terence (1982), "The geometric body in Dürer's engraving Melencolia I", Journal of the Warburg and Courtauld Institutes (The Warburg Institute) 45: 226–232, doi:10.2307/750979, JSTOR 750979 .
  • MacGillavry, C. (1981), "The polyhedron in A. Dürers Melencolia I", Nederl. Akad. Wetensch. Proc. Ser. B 84: 287–294 . As cited by Weitzel (2004).
  • Richter, D. H. (1957), "Perspektive und Proportionen in Albrecht Dürers “Melancholie”", Z. Vermessungswesen 82: 284–288 and 350–357 . As cited by Weitzel (2004).
  • Schreiber, Peter (1999), "A new hypothesis on Dürer's enigmatic polyhedron in his copper engraving “Melencolia I”", Historia Mathematica 26: 369–377, doi:10.1006/hmat.1999.2245 .
  • Schröder, E. (1980), Dürer, Kunst und Geometrie, Dürers künstlerisches Schaffen aus der Sicht seiner “Underweysung”, Basel . As cited by Weitzel (2004).
  • Strauss, Walter L. (1972), The Complete Engravings of Dürer, New York, p. 168, ISBN 0486228517 . As cited by Lynch (1982).
  • Weber, P. (1900), Beiträge zu Dürers Weltanschauung—Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus, Strassburg . As cited by Weitzel (2004).
  • Weitzel, Hans (2004), "A further hypothesis on the polyhedron of A. Dürer's engraving Melencolia I", Historia Mathematica 31 (1): 11–14, doi:10.1016/S0315-0860(03)00029-6 .

Wikimedia Foundation. 2010.

Look at other dictionaries:

  • Dürer — Dürer,   1) Albrecht, Maler, Grafiker, Zeichner und Kunstschriftsteller, * Nürnberg 21. 5. 1471, ✝ ebenda 6. 4. 1528, Bruder von 2). Die Familienchronik, das Tagebuch der niederländischen Reise, Briefe und viele eigenhändige Niederschriften geben …   Universal-Lexikon

  • Albrecht Dürer — The title of this article contains the character ü. Where it is unavailable or not desired, the name may be represented as Albrecht Duerer. Albrecht Dürer Self Portrait (1500) by Albrecht Dürer …   Wikipedia

  • Petersen graph — Infobox graph name = Petersen graph image caption = The Petersen graph is most commonly drawn as a pentagon with a pentagram inside, with five spokes. namesake = Julius Petersen vertices = 10 edges = 15 radius = 2 diameter = 2 girth = 5 chromatic …   Wikipedia

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • List of mathematics articles (C) — NOTOC C C closed subgroup C minimal theory C normal subgroup C number C semiring C space C symmetry C* algebra C0 semigroup CA group Cabal (set theory) Cabibbo Kobayashi Maskawa matrix Cabinet projection Cable knot Cabri Geometry Cabtaxi number… …   Wikipedia

  • soutenir — [ sut(ə)nir ] v. tr. <conjug. : 22> • déb. XIIIe; sostenir Xe; lat. pop. °sustenire, class. sustinere, de sub « sous » et tenere « tenir » I ♦ 1 ♦ Tenir (qqch.) par dessous, en position de stabilité, en …   Encyclopédie Universelle

  • Grafische Sammlung München — Die Staatliche Graphische Sammlung in München gehört zu den wichtigsten Grafik Sammlungen der Welt und ist neben den Kupferstichkabinetten von Berlin und Dresden die bedeutendste Einrichtung dieser Art in Deutschland. Sie beherbergt einen Bestand …   Deutsch Wikipedia

  • Graphische Sammlung München — Die Staatliche Graphische Sammlung in München gehört zu den wichtigsten Grafik Sammlungen der Welt und ist neben den Kupferstichkabinetten von Berlin und Dresden die bedeutendste Einrichtung dieser Art in Deutschland. Sie beherbergt einen Bestand …   Deutsch Wikipedia

  • Muschelkurve — Die Konchoide (v. griech. Muschel) ist eine spezielle ebene Kurve. Sie beschreibt die Bewegung eines Punktes, der – von einem festen Punkt (Pol) aus gesehen – zu einer gegebenen Kurve konstanten Abstand einhält. Inhaltsverzeichnis 1 Eigentliche… …   Deutsch Wikipedia

  • Staatliche Grafische Sammlung München — Die Staatliche Graphische Sammlung in München gehört zu den wichtigsten Grafik Sammlungen der Welt und ist neben den Kupferstichkabinetten von Berlin und Dresden die bedeutendste Einrichtung dieser Art in Deutschland. Sie beherbergt einen Bestand …   Deutsch Wikipedia

Share the article and excerpts

Direct link
https://en-academic.com/dic.nsf/enwiki/11670899 Do a right-click on the link above
and select “Copy Link”