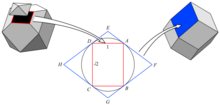
Dual polygon

In geometry, polygons are associated into pairs called duals, where the vertices of one correspond to the edges of the other.

Properties

Dorman Luke construction, showing a rhombus face being dual to a rectangle vertex figure.

Regular polygons are self-dual.

The dual of an isogonal (vertex-transitive) polygon is an isotoxal (edge-transitive) polygon. For example, the (isogonal) rectangle and (isotoxal) rhombus are duals.

In a cyclic polygon, smaller angles correspond to shorter sides, and bigger angles to bigger sides – further, congruent sides in the original yield congruent angles in the dual, and conversely. For example the dual of an acute isosceles triangle is an obtuse isosceles triangle.

In the Dorman Luke construction, each face of a dual polyhedron is the dual polygon of the corresponding vertex figure.

Kinds of duality

Rectification

The simplest qualitative construction of a dual polygon is a rectification operation, where the edges of a polygon are truncated down to vertices at the center of each original edge. New edges are formed between these new vertices.

This construction is not reversible. That is, the polygon generated by applying it twice is not, in general, congruent to the original polygon.

Polar reciprocation

See also: Polar reciprocation

As with dual polyhedra, one can take a circle (be it the inscribed circle, midcircle, or circumscribed circle) and perform polar reciprocation in it.

Projective duality

See also: Dual curve

Under projective duality, the dual of a point is a line, and of a line is a point – thus the dual of a polygon is a polygon, with edges of the original corresponding to vertices of the dual and conversely.

From the point of view of the dual curve, where to each point on a curve one associates the point dual to its tangent line at that point, the projective dual can be interpreted thus:

• every point on a side of a polygon has the same tangent line, which agrees with the side itself – they thus all map to the same vertex in the dual polygon
• at a vertex, the "tangent lines" to that vertex are all lines through that point with angle between the two edges – the dual points to these lines are then the edge in the dual polygon.

Combinatorially

Combinatorially, one can define a polygon as a set of vertices, a set of edges, and an incidence relation (which vertices and edges touch): two adjacent vertices determine an edge, and dually, two adjacent edges determine a vertex. Then the dual polygon is obtained by simply switching the vertices and edges.

Thus for the triangle with vertices {A,B,C} and edges {AB,BC,CA}, the dual triangle has vertices {AB,BC,CA}, and edges {B,C,A}, where B connects AB & BC, and so forth.

This is not a particularly fruitful avenue, as combinatorially, there is a single family of polygons (given by number of sides); geometric duality of polygons is more varied, as are combinatorial dual polyhedra.

See also

• Dual curve
• Dual polyhedron
• Self-dual polygon