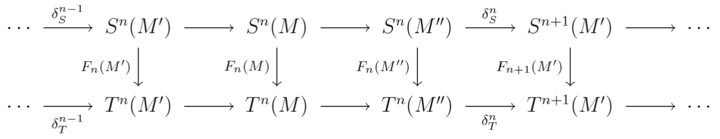Delta-functor

In homological algebra, a δ-functor between two abelian categories A and B is a collection of functors from A to B together with a collection of morphisms that satisfy properties generalising those of derived functors. A universal δ-functor is a δ-functor satisfying a specific universal property related to extending morphisms beyond "degree 0". These notions were introduced by Alexander Grothendieck in his famous "Tohoku" paper to provide an appropriate setting for derived functors.^[1] In particular, derived functors are universal δ-functors.

The terms homological δ-functor and cohomological δ-functor are sometimes used to distinguish between the case where the morphisms "go down" (homological) and the case where they "go up" (cohomological). In particular, one of these modifiers should always be used, but is often dropped.

Definition

Given two abelian categories A and B a covariant cohomological δ-functor between A and B is a family {Tⁿ} of covariant additive functors Tⁿ : A → B indexed by the non-negative integers, and for each short exact sequence

$0\rightarrow M^\prime\rightarrow M\rightarrow M^{\prime\prime}\rightarrow0$

a family of morphisms

$\delta^n:T^n(M^{\prime\prime})\rightarrow T^{n+1}(M^\prime)$

indexed by the non-negative integers satisfying the following two properties:

1. For each short exact sequence as above, there is a long exact sequence

2. For each morphism of short exact sequences

and for each non-negative n, the induced square

is commutative (the δⁿ on the top is that corresponding to the short exact sequence of M's whereas the one on the bottom corresponds to the short exact sequence of N's).

The second property expresses the functoriality of a δ-functor. The modifier "cohomological" indicates that the δⁿ raise the index on the T. A covariant homological δ-functor between A and B is similarly defined (and generally uses subscripts), but with δ_n a morphism T_n(M '') → T_n-1(M'). The notions of contravariant cohomological δ-functor between A and B and contravariant homological δ-functor between A and B can also be defined by "reversing the arrows" accordingly.

Morphisms of δ-functors

A morphism of δ-functors is a family of natural transformations that, for each short exact sequence, commute with the morphisms δ. For example, in the case of two covariant cohomological δ-functors denoted S and T, a morphism from S to T is a family F_n : Sⁿ → Tⁿ of natural transformations such that for every short exact sequence

$0\rightarrow M^\prime\rightarrow M\rightarrow M^{\prime\prime}\rightarrow0$

the following diagram commutes:

Universal δ-functor

A universal δ-functor is characterized by the (universal) property that giving a morphism from it to any other δ-functor (between A and B) is equivalent to giving just F₀. For example, if S denotes a covariant cohomological δ-functor between A and B, then S is universal if given any other (covariant cohomological) δ-functor T (between A and B), and given any natural transformation

$F_0:S^0\rightarrow T^0$

there is a unique sequence F_n indexed by the positive integers such that the family { F_n }_{n ≥ 0} is a morphism of δ-functors.

Notes

1. ^ Grothendieck 1957

References

• Grothendieck, Alexander (1957), "Sur quelques points d'algèbre homologique", The Tôhoku Mathematical Journal. Second series 9 (2-3), MR0102537 

• Section XX.7 of Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR1878556 

• Section 2.1 of Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, ISBN 978-0-521-55987-4, OCLC 36131259, MR1269324