Covering graph

In the mathematical discipline of graph theory, a graph C is a covering graph of another graph G if there is a covering map from the vertex set of C to the vertex set of G. A covering map f is a surjection and a local isomorphism: the neighbourhood of a v vertex in C is mapped bijectively onto the neighbourhood of f(v) in G.

Note that a covering in graph theory may also refer to an unrelated concept, a subset of vertices that touches all edges.

Definition

Let G = (V, E) and C = (V₂, E₂) be two graphs, and let f: V₂ → V be a surjection. Then f is a covering map from C to G if for each v ∈ V₂, the restriction of f to the neighbourhood of v is a bijection onto the neighbourhood of f(v) ∈ V in G. Put otherwise, f maps edges incident to v one-to-one onto edges incident to f(v).

If there exists a covering map from C to G, then C is a covering graph (or a lift) of G.

Examples

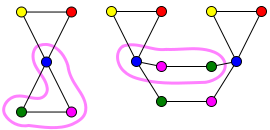
In the following figure, the graph C is a covering graph of the graph H.

The covering map f from C to H is indicated with the colours. For example, both blue vertices of C are mapped to the blue vertex of H. The map f is a surjection: each vertex of H has a preimage in C. Furthermore, f maps bijectively each neighbourhood of a vertex v in C onto the neighbourhood of the vertex f(v) in H.

For example, let v be one of the purple vertices in C; it has two neighbours in C, a green vertex u and a blue vertex t. Similarly, let v′ be the purple vertex in H; it has two neighbours in H, the green vertex u′ and the blue vertex t′. The mapping f restricted to {t, u, v} is a bijection onto {t′, u′, v′}. This is illustrated in the following figure:

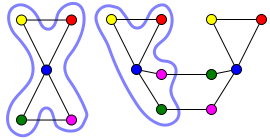
Similarly, we can check that the neighbourhood of a blue vertex in C is mapped one-to-one onto the neighbourhood of the blue vertex in H:

Double cover

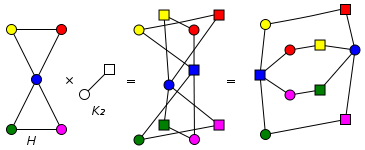
In the above example, each vertex of H has exactly 2 preimages in C. Hence H is a 2-fold cover or a double cover of C.

For any graph G, it is possible to construct the bipartite double cover of G, which is a bipartite graph and a double cover of G. The bipartite double cover of G is the tensor product of graphs G × K₂:

If G is already bipartite, its bipartite double cover consists of two disjoint copies of G. A graph may have many different double covers other than the bipartite double cover.

Universal cover

For any connected graph G, it is possible to construct its universal covering graph.^[1] This is an instance of the more general universal cover concept from topology; the topological requirement that a universal cover be simply connected translates in graph-theoretic terms to a requirement that it be acyclic and connected; that is, a tree. The universal covering graph is unique (up to isomorphism). If G is a tree, then G itself is the universal covering graph of G. For any other finite connected graph G, the universal covering graph of G is a countably infinite (but locally finite) tree.

The universal covering graph T of a connected graph G can be constructed as follows. Choose an arbitrary vertex r of G as a starting point. Each vertex of T is a non-backtracking walk that begins from r, that is, a sequence w = (r, v₁, v₂, ..., v_n) of vertices of G such that

• v_i and v_i+1 are adjacent in G for all i, i.e., w is a walk
• v_i-1 ≠ v_i+1 for all i, i.e., w is non-backtracking.

Then, two vertices of T are adjacent if one is a simple extension of another: the vertex (r, v₁, v₂, ..., v_n) is adjacent to the vertex (r, v₁, v₂, ..., v_n-1). Up to isomorphism, the same tree T is constructed regardless of the choice of the starting point r.

The covering map f maps the vertex (r) in T to the vertex r in G, and a vertex (r, v₁, v₂, ..., v_n) in T to the vertex v_n in G.

Examples of universal covers

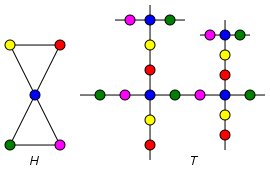
The following figure illustrates the universal covering graph T of a graph H; the colours indicate the covering map.

For any k, all k-regular graphs have the same universal cover: the infinite k-regular tree.

Voltage graphs

A common way to form covering graphs uses voltage graphs, in which the darts of the given graph G (that is, pairs of directed edges corresponding to the undirected edges of G) are labeled with inverse pairs of elements from some group. The derived graph of the voltage graph has as its vertices the pairs (v,x) where v is a vertex of G and x is a group element; a dart from v to w labeled with the group element y in G corresponds to an edge from (v,x) to (w,xy) in the derived graph.

The universal cover can be seen in this way as a derived graph of a voltage graph in which the edges of a spanning tree of the graph are labeled by the identity element of the group, and each remaining pair of darts is labeled by a distinct generating element of a free group. The bipartite double can be seen in this way as a derived graph of a voltage graph in which each dart is labeled by the nonzero element of the group of order two.

Notes

1. ^ Angluin 1980.

References

• Chris Godsil and Gordon Royle: Algebraic Graph Theory, Springer, 2004. Sect. 6.8.
• Alon Amit, Nathan Linial, Jiří Matoušek, and Eyal Rozenman: "Random lifts of graphs", Proc. SODA 2001, p. 883–894.
• Dana Angluin: "Local and global properties in networks of processors", Proc. STOC 1980, p. 82–93.