Graph factorization

Not to be confused with Factor graph.

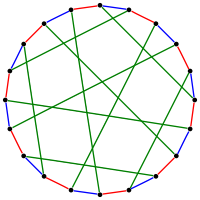1-factorization of Desargues graph: each color class is a 1-factor.

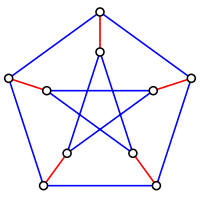Petersen graph can be partitioned into a 1-factor (red) and a 2-factor (blue). However, the graph is not 1-factorable.

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is an edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.

1-factorization

If a graph is 1-factorable, then it has to be a regular graph. However, not all regular graphs are 1-factorable. A k-regular graph is 1-factorable if it has chromatic index k; examples of such graphs include:

• Any regular bipartite graph.^[1] Hall's marriage theorem can be used to show that a k-regular bipartite graph contains a perfect matching. One can then remove the perfect matching to obtain a (k − 1)-regular bipartite graph, and apply the same reasoning repeatedly.
• Any complete graph with an even number of nodes (see below).^[2]

However, there are also k-regular graphs that have chromatic index k + 1, and these graphs are not 1-factorable; examples of such graphs include:

• Any regular graph with an odd number of nodes.
• Petersen graph.

Complete graphs

An easy to generate 1-factorization of K₈. Each set of edges with the same color is a 1-factor.

Draw seven vertices distributed evenly around a circle, and one in the middle, for a total of eight vertices. Join the middle point to any single point on the circle; call this line L. Join points to other points on the circle together if and only if they can be joined together with a line orthogonal to L. Since the points were arranged evenly, this will produce a matching (in fact a perfect matching) of these eight vertices.

Now rotate the lines one vertex to the right: Start over again with the eight vertices as described and join the center point to the point in the circle directly clockwise from the first one chosen. Join the other points on the circle in a similar manner as before. This is again another perfect matching of these eight points.

Each of these perfect matchings can also be looked at as a 1-factor of the complete graph on eight vertices, K₈. Continuing the process above, you will form a 1-factorization of K₈. This is a proof that there exists a 1-factorization of K_2n for all n.

A 1-factorization of a complete graph corresponds to pairings in a round-robin tournament. The 1-factorization of complete graphs is a special case of Baranyai's theorem concerning the 1-factorization of complete hypergraphs.

1-factorization conjecture

Let G be a k-regular graph with 2n nodes. If k is sufficiently large, it is known that G has to be 1-factorable:

• If k = 2n − 1, then G is the complete graph K_2n, and hence 1-factorable (see above).
• If k = 2n − 2, then G can be constructed by removing a perfect matching from K_2n. Again, G is 1-factorable.
• Chetwynd & Hilton (1985) show that if k ≥ 12n/7, then G is 1-factorable.

The 1-factorization conjecture^[3] is a long-standing conjecture that states that k ≈ n is sufficient. In precise terms, the conjecture is:

• If n is odd and k ≥ n, then G is 1-factorable. If n is even and k ≥ n − 1 then G is 1-factorable.

The overfull conjecture implies the 1-factorization conjecture.

2-factorization

If a graph is 2-factorable, then it has to be 2k-regular for some integer k. Julius Petersen showed in 1891 that this necessary condition is also sufficient: any 2k-regular graph is 2-factorable.^[4]

If a graph is 2k-regular it may also be k-factored, by choosing each of the two factors to be an alternating subset of the edges of an Euler tour.^[5]

Notes

1. ^ Harary (1969), Theorem 9.2, p. 85. Diestel (2005), Corollary 2.1.3, p. 37.
2. ^ Harary (1969), Theorem 9.1, p. 85.
3. ^ Chetwynd & Hilton (1985). Niessen (1994). Perkovic & Reed (1997). West.
4. ^ Petersen (1891), §9, p. 200. Harary (1969), Theorem 9.9, p. 90. See Diestel (2005), Corollary 2.1.5, p. 39 for a proof.
5. ^ Petersen (1891), §6, p. 198.

References

• Bondy, John Adrian; Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, ISBN 0-444-19451-7, http://www.ecp6.jussieu.fr/pageperso/bondy/books/gtwa/gtwa.html , Section 5.1: "Matchings".
• Chetwynd, A. G.; Hilton, A. J. W. (1985), "Regular graphs of high degree are 1-factorizable", Proceedings of the London Mathematical Society 50 (2): 193–206, doi:10.1112/plms/s3-50.2.193 .
• Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6 , Chapter 2: "Matching, covering and packing". Electronic edition.
• Harary, Frank (1969), Graph Theory, Addison-Wesley, ISBN 0-201-02787-9 , Chapter 9: "Factorization".
• Niessen, Thomas (1994), "How to find overfull subgraphs in graphs with large maximum degree", Discrete Applied Mathematics 51 (1–2): 117–125, doi:10.1016/0166-218X(94)90101-5 .
• Perkovic, L.; Reed, B. (1997), "Edge coloring regular graphs of high degree", Discrete Mathematics 165–166: 567–578, doi:10.1016/S0012-365X(96)00202-6 .
• Petersen, Julius (1891), "Die Theorie der regulären graphs", Acta Mathematica 15: 193–220, doi:10.1007/BF02392606 .
• West, Douglas B.. "1-Factorization Conjecture (1985?)". Open Problems – Graph Theory and Combinatorics. http://www.math.uiuc.edu/~west/openp/1fact.html. Retrieved 2010-01-09. 
• Weisstein, Eric W., "Graph Factor" from MathWorld.
• Weisstein, Eric W., "k-Factor" from MathWorld.
• Weisstein, Eric W., "k-Factorable Graph" from MathWorld.

Further reading

• Plummer, Michael D. (2007), "Graph factors and factorization: 1985–2003: A survey", Discrete Mathematics 307 (7–8): 791–821, doi:10.1016/j.disc.2005.11.059 .