- Āryabhaṭa's sine table
-
Āryabhaṭa's sine table is a set of twenty-four of numbers given in the astronomical treatise Āryabhaṭiya composed by the fifth century Indian mathematician and astronomer Āryabhaṭa (476–550 CE), for the computation of the half-chords of certain set of arcs of a circle. It is not a table in the modern sense of a mathematical table; that is, it is not a set of numbers arranged into rows and columns.[1]
It is only a collection of numbers appearing as a Sanskrit stanza in Āryabhaṭiya and is couched in the special numerical notation invented by Āryabhaṭa himself. This stanza is the tenth one (excluding the stanza containing the invocation and a stanza which is an explanation of Āryabhaṭa's numerical notation) in the first section of Āryabhatiya titled Daśagītikasūtra.[2] Āryabhaṭa's table is also not a set of values of the trigonometric sine function in a conventional sense; it is a table of the first differences of the values of trigonometric sines expressed in arcminutes, and because of this the table is also referred to as Āryabhaṭa's table of sine-differences.[3][4]
Āryabhaṭa's table was the first sine table ever constructed in the history of mathematics.[5] The now lost tables of Hipparchus (c.190 BC – c.120 BC) and Menelaus (c.70–140 CE) and those of Ptolemy (c.AD 90 – c.168) were all tables of chords and not of half-chords.[5] Āryabhaṭa's table remained as the standard sine table of ancient India. There were continuous attempts to improve the accuracy of this table. These endeavors culminated in the eventual discovery of the power series expansions of the sine and cosine functions by Madhava of Sangamagrama (c.1350 – c.1425), the founder of the Kerala school of astronomy and mathematics, and the tabulation of a sine table by Madhava with values accurate to seven or eight decimal places.
Some historians of mathematics have argued that the sine table given in Āryabhaṭiya was an adaptation of earlier such tables constructed by mathematicians and astronomers of ancient Greece.[6] David Pingree, one of America's foremost historians of the exact sciences in antiquity, was an exponent of such a view. Assuming this hypothesis, G. J. Toomer[7] even tried to reconstruct Hipparchus's table of chords from similar tables found in Indian treatises.[8] The inadequacies and imperfections in these arguments have also been pointed by several scholars.[9][10] "Hardly any documentation exists for the earliest arrival of Greek astronomical models in India, or for that matter what those models would have looked like. So it is very difficult to ascertain the extent to which what has come down to us represents transmitted knowledge, and what is original with Indian scientists. ... The truth is probably a tangled mixture of both."[11]
Contents
The table
The original table
The stanza in Āryabhaṭiya describing the sine table is reproduced below:
मखि भखि फखि धखि णखि ञखि ङखि हस्झ स्ककि किष्ग श्घकि किघ्व |
घ्लकि किग्र हक्य धकि किच स्ग झश ङ्व क्ल प्त फ छ कला-अर्ध-ज्यास् ||In modern notations
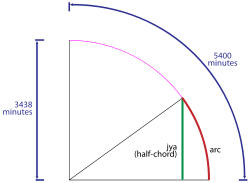
The values encoded in Āryabhaṭa's Sanskrit verse can be decoded using the numerical scheme explained in Aryabhatiya, and the decoded numbers are listed in the table below. In the table, the angle measures relevant to Āryabhaṭa's sine table are listed in the second column. The third column contains the list the numbers contained in the Sanskrit verse given above in Devanagari script. For the convenience of users unable to read Devanagari, these word-numerals are reproduced in the fourth column in ISO 15919 transliteration. The next column contains these numbers in the Arabic numerals. Āryabhaṭa's numbers are the first differences in the values of sines. The corresponding value of sine (or more precisely, of jya) can be obtained by summing up the differences up to that difference. Thus the value of jya corresponding to 18° 45′ is the sum 225 + 224 + 222 + 219 + 215 = 1105. For assessing the accuracy of Āryabhaṭa's computations, the modern values of jyas are given in the last column of the table.
In the Indian mathematical tradition, the sine ( or jya) of an angle is not a ratio of numbers. It is the length of a certain line segment, a certain half-chord. The radius of the base circle is basic parameter for the construction of such tables. Historically, several tables have been constructed using different values for this parameter. Āryabhaṭa has chosen the number 3438 as the value of radius of the base circle for the computation of his sine table. The rationale of the choice of this parameter is the idea of measuring the circumference of a circle in angle measures. In astronomical computations distances are measured in degrees, minutes, seconds, etc. In this measure, the circumference of a circle is 360° = (60 × 360) minutes = 21600 minutes. The radius of the circle, the measure of whose circumference is 21600 minutes, is 21600 / 2π minutes. Computing this using the value π = 3.1416 known to Aryabhata one gets the radius of the circle as 3438 minutes approximately. Āryabhaṭa's sine table is based on this value for the radius of the base circle. It has not yet been established who is the first ever to use this value for the base radius. But Aryabhatiya is the earliest surviving text containing a reference to this basic constant.[12]
Sl. No Angle ( A )
(in degrees,
arcminutes)Value in Āryabhaṭa's
numerical notation
(in Devanagari)Value in Āryabhaṭa's
numerical notation
(in ISO 15919 transliteration)Value in
Arabic numeralsĀryabhaṭa's
value of
jya (A)Modern value
of jya (A)
(3438 × sin (A))1 03° 45′ मखि makhi 225 225′ 224.8560 2 07° 30′ भखि bhakhi 224 449′ 448.7490 3 11° 15′ फखि phakhi 222 671′ 670.7205 4 15° 00′ धखि dhakhi 219 890′ 889.8199 5 18° 45′ णखि ṇakhi 215 1105′ 1105.1089 6 22° 30′ ञखि ñakhi 210 1315′ 1315.6656 7 26° 15′ ङखि ṅakhi 205 1520′ 1520.5885 8 30° 00′ हस्झ hasjha 199 1719′ 1719.0000 9 33° 45′ स्ककि skaki 191 1910′ 1910.0505 10 37° 30′ किष्ग kiṣga 183 2093′ 2092.9218 11 41° 15′ श्घकि śghaki 174 2267′ 2266.8309 12 45° 00′ किघ्व kighva 164 2431′ 2431.0331 13 48° 45′ घ्लकि ghlaki 154 2585′ 2584.8253 14 52° 30′ किग्र kigra 143 2728′ 2727.5488 15 56° 15′ हक्य hakya 131 2859′ 2858.5925 16 60° 00′ धकि dhaki 119 2978′ 2977.3953 17 63° 45′ किच kica 106 3084′ 3083.4485 18 67° 30′ स्ग sga 93 3177′ 3176.2978 19 71° 15′ झश jhaśa 79 3256′ 3255.5458 20 75° 00′ ङ्व ṅva 65 3321′ 3320.8530 21 78° 45′ क्ल kla 51 3372′ 3371.9398 22 82° 30′ प्त pta 37 3409′ 3408.5874 23 86° 15′ फ pha 22 3431′ 3430.6390 24 90° 00′ छ cha 7 3438′ 3438.0000 Āryabhaṭa's computational method
The second section of Āryabhaṭiya titled Ganitapāda contains a stanza indicating a method for the computation of the sine table. There are several ambiguities in correctly interpreting the meaning of this verse. For example, the following is a translation of the verse given by Katz wherein the words in square brackets are insertions of the translator and not translations of texts in the verse.[12]
- "When the second half-[chord] partitioned is less than the first half-chord, which is [approximately equal to] the [corresponding] arc, by a certain amount, the remaining [sine-differences] are less [than the previous ones] each by that amount of that divided by the first half-chord."
Without any additional assumptions, no interpretation of this computational scheme has correctly yielded all the numbers in the table compiled by Āryabhaṭa in Āryabhaṭiya.
See also
- Madhava's sine table
- Bhaskara I's sine approximation formula
References
- ^ Helaine Selin (Ed.) (2008). Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures (2 ed.). Springer. pp. 986–988. ISBN 978-1-4020-4425-0.
- ^ Walter Eugene Clark (1930). The Āryabhaṭiya of Āryabhaṭa: An ancient Indian work on mathematics and astronomy. Chicago: The University of Chicago Press.
- ^ Takao Hayashi, T (November 1997). "Āryabhaṭa's rule and table for sine-differences". Historia Mathematica 24 (4): 396–406. doi:10.1006/hmat.1997.2160.
- ^ B. L. van der Waerden, B. L. (March 1988). "Reconstruction of a Greek table of chords". Archive for History of Exact Sciences (Berlin: Springer) 38 (1): 23–38. doi:10.1007/BF00329978.
- ^ a b J J O'Connor and E F Robertson (June 1996). "The trigonometric functions". http://www-history.mcs.st-andrews.ac.uk/HistTopics/Trigonometric_functions.html. Retrieved 4 March 2010.
- ^ "Hipparchus and Trigonometry". http://131.111.104.4/starry/hippmaths.html. Retrieved 6 March 2010.
- ^ G. J. Toomer, G. J. (July 2007 (online)). "The Chord Table of Hipparchus and the Early History of Greek Trigonometry". Centaurus 18 (1): 6–28. doi:10.1111/j.1600-0498.1974.tb00205.x. http://www3.interscience.wiley.com/journal/120069084/abstract?CRETRY=1&SRETRY=0.
- ^ Pingree, David (1976). "The Recovery of Early Greek Astronomy from India". Journal for the History of Astronomy 7: 109–123. Bibcode 1976JHA.....7..109P.
- ^ B.N. Narahari Achar (2002). "Āryabhata and the table of Rsines". Indian Journal of History of Science 37 (2): 95–99. http://www.new.dli.ernet.in/rawdataupload/upload/insa/INSA_1/2000616e_95.pdf. Retrieved 6 March 2010.
- ^ Glen Van Brummelen (March 2000). "[HM Radian Measure"]. Historia Mathematica mailing List Archive. http://sunsite.utk.edu/math_archives/.http/hypermail/historia/mar00/0038.html. Retrieved 6 March 2010.
- ^ Glen Van Brummelen (2009). The mathematics of the heavens and the earth: the early history of trigonometry. Princeton University Press. ISBN 978-0-691-12973-0. http://press.princeton.edu/titles/8956.html.
- ^ a b Victor J Katz (Editor) (2007). The mathematics of Egypt, Mesopotamia, China, India, and Islam: a sourcebook. Princeton: Princeton University Press. pp. 405–408. ISBN 0691114854.
Categories:
Wikimedia Foundation. 2010.