Clifford's circle theorems
- Clifford's circle theorems
-
In geometry, Clifford's theorems, named after the English geometer William Kingdon Clifford, are a sequence of theorems relating to intersections of circles.
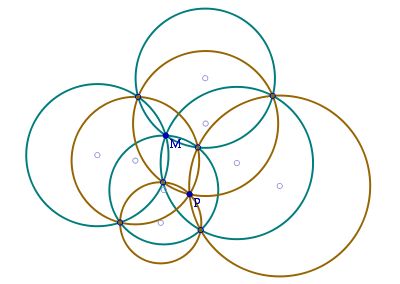
The first theorem considers any four circles passing through a common point M. Four new circles can be constructed to pass through their other intersection points taken in triplets, so that each intersection's triple touches three circles only. Then these four circles also pass through a single point P.
The second theorem considers five circles passing through a single point M. Each subset of four circles defines a new point P according to the first theorem. Then these five points all lie on a single circle C.
The third theorem consider six circles that pass through a single point M. Each subset of five circles defines a new circle by the second theorem. Then these six new circles C all pass through a single point.
The sequence of theorems can be continued indefinitely.
Bibliography
- Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 32–33. ISBN 0-14-011813-6.
External links
Categories: - Circles
- Theorems in geometry
Wikimedia Foundation.
2010.
Look at other dictionaries:
List of circle topics — This list of circle topics includes things related to the geometric shape, either abstractly, as in idealizations studied by geometers, or concretely in physical space. It does not include metaphors like inner circle or circular reasoning in… … Wikipedia
List of mathematics articles (C) — NOTOC C C closed subgroup C minimal theory C normal subgroup C number C semiring C space C symmetry C* algebra C0 semigroup CA group Cabal (set theory) Cabibbo Kobayashi Maskawa matrix Cabinet projection Cable knot Cabri Geometry Cabtaxi number… … Wikipedia
Archimedes — For other uses, see Archimedes (disambiguation). Archimedes of Syracuse (Greek: Ἀρχιμήδης) … Wikipedia
Introduction to general relativity — General relativity (GR) is a theory of gravitation that was developed by Albert Einstein between 1907 and 1915. According to general relativity, the observed gravitational attraction between masses results from the warping of space and time by… … Wikipedia
Supergravity — In theoretical physics, supergravity (supergravity theory) is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry (in contrast to… … Wikipedia
Geometric algebra — In mathematical physics, a geometric algebra is a multilinear algebra described technically as a Clifford algebra over a real vector space equipped with a non degenerate quadratic form. Informally, a geometric algebra is a Clifford algebra that… … Wikipedia
Split-complex number — A portion of the split complex number plane showing subsets with modulus zero (red), one (blue), and minus one (green). In abstract algebra, the split complex numbers (or hyperbolic numbers) are a two dimensional commutative algebra over the real … Wikipedia
Michael Atiyah — Sir Michael Atiyah Born 22 April 1929 (1929 04 22) (age 82) … Wikipedia
Otto Neurath — Otto Karl Wilhelm Neurath Full name Otto Karl Wilhelm Neurath Born December 10, 1882(1882 12 10) Vienna, Austro Hungarian Empire (now in Austria) Died December 22, 1945(1945 12 22) (aged 63) Oxford, UK … Wikipedia
Manifold — For other uses, see Manifold (disambiguation). The sphere (surface of a ball) is a two dimensional manifold since it can be represented by a collection of two dimensional maps. In mathematics (specifically in differential geometry and topology),… … Wikipedia