Miquel's theorem

A diagram showing circles passing through the vertices of a triangle ABC and points A´, B´ and C´ on the adjacent sides of the triangle intersecting at a common point, M.

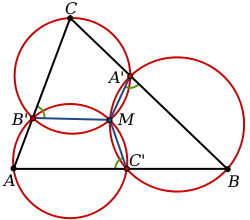
Miquel's theorem is a theorem in geometry, named after Auguste Miquel, about the intersection pattern of circles defined from six points on a triangle. From any triangle, and any three points on the three sides of the triangle, one may define three circles that each pass through a vertex of the triangle and the two points on its adjacent sides; Miquel's theorem states that these three circles meet in a single point, called the Miquel point.

Formally, let ABC be a triangle, and let A´, B´ and C´ be three points on sides BC, AC, and AB of the triangle, respectively. Draw three circles circumscribing the three triangles AB´C´, A´BC´, and A´B´C. Then Miquel's theorem states that these three circles intersect in a single point M, the Miquel point. In addition, the three angles MA´B, MB´C and MC´A (green in the diagram) are all equal to each other, as are the three angles MA´C, MB´A and MC´B.

If the fractional distances of points A´, B´ and C´ along the sides BC, CA and AB are respectively d_a, d_b and d_c, and $d_x^{\,'} = 1- d_x$, the Miquel point is given in trilinear co-ordinates (x : y : z) by:

$x=a \left(-a^2 d_a d_a^{\,'} + b^2 d_a d_b + c^2 d_a^{\,'} d_c^{\,'} \right)$

$y=b \left(a^2 d_a^{\,'} d_b^{\,'} - b^2 d_b d_b^{\,'} + c^2 d_b d_c \right)$

$z=c \left(a^2 d_a d_c + b^2 d_b^{\,'} d_c^{\,'} - c^2 d_c d_c^{\,'} \right).$

In the case $d_a = d_b = d_c = \frac{1}{2}$, the Miquel point is the circumcentre.

This theorem can be reversed to say that for any three circles intersecting at M, a line can be drawn from any point A on one of the circles, through C´ to the intersection, B, with another circle. This point is then connected to a point C of the third circle with a line passing through A´. Given this construction, C, B´ and A are collinear. That is to say, the triangle ABC will always pass though the points A´, B´ and C´.

Miquel's six circles theorem states that if five circles share four triple-points of intersection then the remaining four points of intersection lie on a sixth circle.

This can be extended to a circle with four points. Given four points, A, B, C, and D on a circle, and four circles passing through each adjacent pair of points, the four intersections of adjacent circles (i.e., the circle pairs also sharing an intersection on the original circle) W, X, Y and Z also lie on a common circle. This result is known as Miquel's six circles theorem.

See also

• Pivot theorem

Bibliography

• Wells, David (1991), The Penguin Dictionary of Curious and Interesting Geometry, New York: Penguin Books, pp. 151–152, ISBN 0-14-011813-6 
• Miquel, Auguste (1838), "Mémoire de Géométrie", Journal de mathématiques pures et appliquées de Liouville 1: 485–487 .

External links

• Weisstein, Eric W., "Miquel's theorem" from MathWorld.
• Miquels' Theorem as a special case of a generalization of Napoleon's Theorem at Dynamic Geometry Sketches