- Compound of ten octahedra
-
Compounds of ten octahedra 
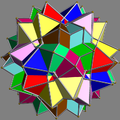
Type Uniform compound Index UC15 and UC16 Polyhedra 10 octahedra Faces 20+60 triangles Edges 120 Vertices 60 Symmetry group icosahedral (Ih) Subgroup restricting to one constituent 3-fold antiprismatic (D3d) These uniform polyhedron compounds are symmetric arrangements of 10 octahedra, considered as triangular antiprisms, aligned with the axes of three-fold rotational symmetry of an icosahedron. The two compounds differ in the orientation of their octahedra: each compound may be transformed into the other by rotating each octahedron by 60 degrees.
Cartesian coordinates
Cartesian coordinates for the vertices of this compound are all the cyclic permutations of
- (0, ±(τ−1√2 + 2sτ), ±(τ√2 − 2sτ−1))
- (±(√2 − sτ2), ±(√2 + s(2τ − 1)), ±(√2 + sτ−2))
- (±(τ−1√2 − sτ), ±(τ√2 + sτ−1), ±3s)
where τ = (1 + √5)/2 is the golden ratio (sometimes written φ) and s is either +1 or −1. Setting s = −1 gives UC15, while s = +1 gives UC16.
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society 79: 447–457, doi:10.1017/S0305004100052440, MR0397554.

This polyhedron-related article is a stub. You can help Wikipedia by expanding it.
