- Compound of five truncated tetrahedra
-
Compound of five truncated tetrahedra 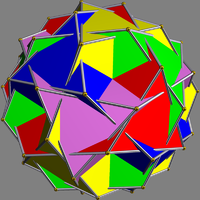
Type Uniform compound Index UC55 Polyhedra 5 truncated tetrahedra Faces 20 triangles, 20 hexagons Edges 90 Vertices 60 Dual Compound of five triakis tetrahedra Symmetry group chiral icosahedral (I) Subgroup restricting to one constituent chiral tetrahedral (T) This uniform polyhedron compound is a composition of 5 truncated tetrahedra, formed by truncating each of the tetrahedra in the compound of 5 tetrahedra. A far-enough truncation creates the Compound of five octahedra. Its convex hull is a nonuniform Snub dodecahedron.
Cartesian coordinates
Cartesian coordinates for the vertices of this compound are all the cyclic permutations of
- (±1, ±1, ±3)
- (±τ−1, ±(−τ−2), ±2τ)
- (±τ, ±(−2τ−1), ±τ2)
- (±τ2, ±(−τ−2), ±2)
- (±(2τ−1), ±1, ±(2τ−1))
with an even number of minuses in the choices for '±', where τ = (1+√5)/2 is the golden ratio (sometimes written φ).
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society 79: 447–457, doi:10.1017/S0305004100052440, MR0397554.

This polyhedron-related article is a stub. You can help Wikipedia by expanding it.
