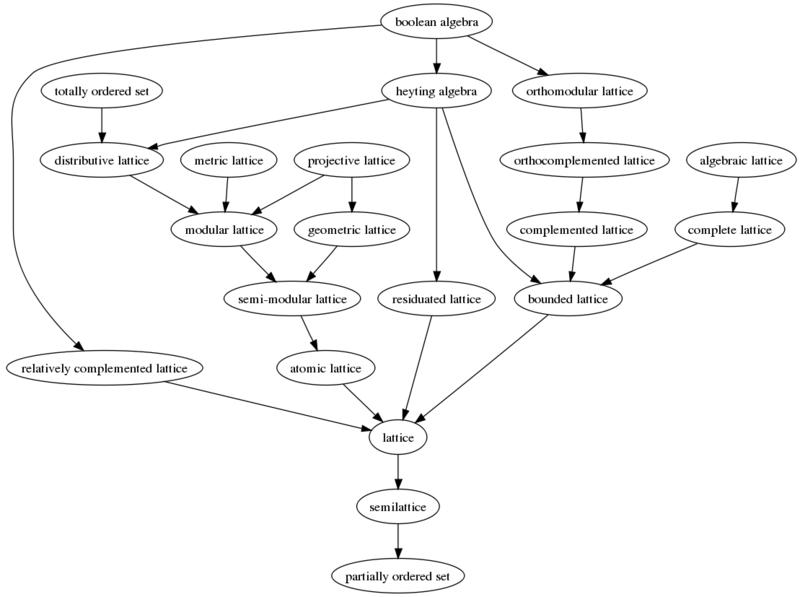
Map of lattices

Map of lattices

The concept of a lattice arises in order theory, a branch of mathematics. The Hasse diagram below depicts the inclusion relationships among some important subclasses of lattices.

Lattice v4.png

Proofs of the relationships in the map

1. A boolean algebra is a complemented distributive lattice. (def)

2. A boolean algebra is a heyting algebra.[1]

3. A boolean algebra is orthocomplemented.[2]

4. A distributive orthocomplemented lattice is orthomodular.[3]

5. A boolean algebra is orthomodular. (1,3,4)

6. An orthomodular lattice is orthocomplemented. (def)

7. An orthocomplemented lattice is complemented. (def)

8. A complemented lattice is bounded. (def)

9. An algebraic lattice is complete. (def)

10. A complete lattice is bounded.

11. A heyting algebra is bounded. (def)

12. A bounded lattice is a lattice. (def)

13. A heyting algebra is residuated.

14. A residuated lattice is a lattice. (def)

15. A distributive lattice is modular.[4]

16. A modular complemented lattice is relatively complemented.[5]

17. A boolean algebra is relatively complemented. (1,15,16)

18. A relatively complemented lattice is a lattice. (def)

19. A heyting algebra is distributive.[6]

20. A totally ordered set is a distributive lattice.

21. A metric lattice is modular.[7]

22. A modular lattice is semi-modular.[8]

23. A projective lattice is modular.[9]

24. A projective lattice is geometric. (def)

25. A geometric lattice is semi-modular.[10]

26. A semi-modular lattice is atomic.[11]

27. An atomic lattice is a lattice. (def)

28. A lattice is a semi-lattice. (def)

29. A semi-lattice is a partially ordered set. (def)

Notes

  1. ^ Rutherford (1965), p.77.
  2. ^ Rutherford (1965), p.32-33.
  3. ^ PlanetMath: orthomodular lattice
  4. ^ Rutherford (1965), p.22.
  5. ^ Rutherford (1965), p.31.
  6. ^ Rutherford (1965), Th.25.1 p.74.
  7. ^ Rutherford (1965), Th.8.1 p.22.
  8. ^ Rutherford (1965), p.87.
  9. ^ Rutherford (1965), p.94.
  10. ^ Rutherford (1965), Th.32.1 p.92.
  11. ^ Rutherford (1965), p.89.

References

  • Rutherford, Daniel Edwin (1965). Introduction to Lattice Theory. Oliver and Boyd. 

Wikimedia Foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Look at other dictionaries:

  • Coupled map lattice — A coupled map lattice (CML) is a dynamical system that models the behavior of non linear systems (especially partial differential equations). They are predominantly used to qualitatively study the chaotic dynamics of spatially extended systems.… …   Wikipedia

  • Duality theory for distributive lattices — In mathematics, duality theory for distributive lattices provides three different (but closely related) representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces. This generalizes the well… …   Wikipedia

  • Lattice (order) — See also: Lattice (group) The name lattice is suggested by the form of the Hasse diagram depicting it. Shown here is the lattice of partitions of a four element set {1,2,3,4}, ordered by the relation is a refinement of . In mathematics, a… …   Wikipedia

  • List of mathematics articles (M) — NOTOC M M estimator M group M matrix M separation M set M. C. Escher s legacy M. Riesz extension theorem M/M/1 model Maass wave form Mac Lane s planarity criterion Macaulay brackets Macbeath surface MacCormack method Macdonald polynomial Machin… …   Wikipedia

  • Free lattice — In mathematics, in the area of order theory, a free lattice is the free object corresponding to a lattice. As free objects, they have the universal property. The word problem for free lattices is also challenging.Formal definitionAny set X may be …   Wikipedia

  • Algebraic torus — In mathematics, an algebraic torus is a type of commutative affine algebraic group. These groups were named by analogy with the theory of tori in Lie group theory (see maximal torus). The theory of tori is in some sense opposite to that of… …   Wikipedia

  • Outline of algebraic structures — In universal algebra, a branch of pure mathematics, an algebraic structure is a variety or quasivariety. Abstract algebra is primarily the study of algebraic structures and their properties. Some axiomatic formal systems that are neither… …   Wikipedia

  • Bass–Serre theory — is a part of the mathematical subject of group theory that deals with analyzing the algebraic structure of groups acting by automorphisms on simplicial trees. The theory relates group actions on trees with decomposing groups as iterated… …   Wikipedia

  • Congruence lattice problem — In mathematics, the congruence lattice problem asks whether every algebraic distributive lattice is isomorphic to the congruence lattice of some other lattice. The problem was posed by Robert P. Dilworth, and for many years it was one of the most …   Wikipedia

  • Interior algebra — In abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”