- Static light scattering
-
Static light scattering is a technique in physical chemistry that measures the intensity of the scattered light to obtain the average molecular weight Mw of a macromolecule like a polymer or a protein. Measurement of the scattering intensity at many angles allows calculation of the root mean square radius, also called the radius of gyration Rg. By measuring the scattering intensity for many samples of various concentrations, the second virial coefficient A2, can be calculated.[1][2][3][4][5]
For static light scattering experiments, a high intensity monochromatic light, usually a laser, is launched in a solution containing the macromolecules. One or many detectors are used to measure the scattering intensity at one or many angles.
In order to measure the weight average molecular weight directly, without calibration, from the light scattering intensity, the laser intensity, the quantum efficiency of the detector and the full scattering volume and solid angle of the detector needs to be known. Since this is impractical, all commercial instruments are calibrated using a strong, known scatterer like toluene since the Rayleigh Ratio of toluene and a few other solvents were measured using an absolute light scattering instrument.
Contents
Theory
For a light scattering instrument composed of many detectors placed at various angles, all the detectors need to respond the same way. Usually detectors will have slightly different quantum efficiency, different gains and are looking at different geometrical scattering volumes. In this case a normalization of the detectors is absolutely needed. To normalize the detectors, a measurement of a pure solvent is made first. Then an isotropic scatterer is added to the solvent. Since isotropic scatterers scatter the same intensity at any angle, the detector efficiency and gain can be normalized with this procedure. It is convenient to normalize all the detectors to the 90° angle detector.

where IR(90) is the scattering intensity measured for the Rayleigh scatterer by the 90° angle detector.
The most common equation to measure the weight average molecular weight, Mw, is the Zimm equation:

where

and

with

and the scattering vector for vertically polarized light is

with n0 the refractive index of the solvent, λ the wavelength of the light source, dn/dc the refactive index increment of the solution, NA is Avogadro's number (6.023x1023) and c the solution concentration. The intensity of the analyte measured at an angle is IA(θ). In these equation the subscript A is for analyte (the solution) and T is for the toluene with the Rayleigh Ratio of toluene, RT being 1.35x10−5 cm−1 for a HeNe laser. As described above, the radius of gyration, Rg, and the second virial coefficient, A2, are also calculated from this equation.
A Zimm plot is built from a double extrapolation to zero angle and zero concentration from many angle and many concentration measurements. In the most simple form, the Zimm equation is reduced to:

for measurements made at low angle and infinite dilution since P(0) = 1.
There are typically a number of analyses developed to analyze the scattering of particles in solution to derive the above named physical characteristics of particles. A simple static light scattering experiment entails the average intensity of the sample that is corrected for the scattering of the solvent will yield the Rayleigh ratio, R as a function of the angle or the wave vector q as follows:
Data Analyses
Guinier plot
The scattered intensity can be plotted as a function of the angle to give information on the Rg which can simply be calculated using the Guinier approximation as follows:

where ln(ΔR(θ)) = lnP(θ) also known as the form factor with q = 4πn0sin(θ/2)/λ. Hence a plot of the corrected Rayleigh ratio, ΔR(θ) vs sin(θ/2) or q2 will yield a slope Rg2/3. However, this approximation is only true for qRg < 1. Note that for a Guinier plot, the value of dn/dc and the concentration is not needed.
Kratky plot
The Kratky plot is typically used to analyze the conformation of proteins, but can be used to analyze the random walk model of polymers. A Kratky plot can be made by plotting sin2(θ/2)ΔR(θ) vs sin(θ/2) or q2ΔR(θ) vs q.
Debye plot
This method is used to derive the molecular mass and 2nd virial coefficient, A2, of the polymer or polymer complex system. The difference to the Zimm plot is that the experiments are performed using a single angle. Since only one angle is used (typically 90o), the Rg cannot be determined as can be seen from the following equation:

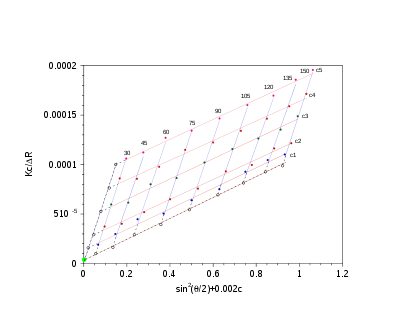
Zimm plot
For polymers and polymer complexes which are of a monodisperse nature (
 ) as determined by dynamic light scattering, a Zimm plot is a conventional means of deriving the parameters such as Rg, molecular mass Mw and the second virial coefficient A2.
) as determined by dynamic light scattering, a Zimm plot is a conventional means of deriving the parameters such as Rg, molecular mass Mw and the second virial coefficient A2.One must note that if the material constant K defined above is not implemented, a Zimm plot will only yield Rg. Hence implementing K will yield the following equation:

Experiments are performed at several angles and at least 4 concentrations. Performing a Zimm analysis on a single concentration is known as a partial Zimm analysis and is only valid for dilute solutions of strong point scatterers. The partial Zimm however, does not yield the second virial coefficient, due to the absence of the variable concentration of the sample.
References
- ^ A. Einstein (1910). Ann. Phys. 33: 1275.
- ^ C.V. Raman (1927). Indian J. Phys. 2: 1.
- ^ P.Debye (1944). "Light Scattering in Solutions". J. Appl. Phys. 15 (4): 338. doi:10.1063/1.1707436.
- ^ B.H. Zimm (1945). "Molecular Theory of the Scattering of Light in Fluids". J. Chem. Phys. 13 (4): 141. doi:10.1063/1.1724013.
- ^ B.H. Zimm (1948). "The Scattering of Light and the Radial Distribution Function of High Polymer Solutions". J. Chem. Phys. 16 (12): 1093. doi:10.1063/1.1746738.
See also
- Dynamic light scattering
- Light scattering
- Protein-protein interactions
Categories:- Scattering, absorption and radiative transfer (optics)
- Scattering
- Polymer chemistry
- Polymer physics
- Physical chemistry
- Physics
Wikimedia Foundation. 2010.