- Ambiguity function
In pulsed
radar andsonar signal processing, an ambiguity function isa two-dimensional function of time delay and Doppler frequency showing thedistortion of an uncompensatedmatched filter (sometimes calledpulse compression ) due to theDoppler shift of the return from a moving target. The ambiguityfunction is determined by the properties of the pulse used, and not anyparticular target scenario. Many definitions of the ambiguity function exist; Some are restricted to narrowband signals and others are suitable to describe the propagation delay and Doppler relationship of wideband signals. Often the definition of the ambiguity function is given as the magnitude squared of other definitions (Weiss). For a given complexbaseband pulse , the narrowband ambiguity function is given by:
where denotes the
complex conjugate and is theimaginary unit . Note that for zero Doppler shift () this reduces to theautocorrelation of . A more concise way of representing theambiguity function consists of examining the one-dimensionalzero-delay and zero-Doppler "cuts"; that is, and, respectively. The matched filter output as a function of a time (the signal one would observe in a radar system) is a delay cut, with constant frequency given by the target's Doppler shift: .Wideband ambiguity function
The wideband ambiguity function of is (Sibul and Ziomek, 1981 in Weiss, 1994)
:
where "" is a time scale factor of the received signal relative to the transmitted signal given by:
:
for an object moving with constant radial velocity "v".
Ideal ambiguity function
An ambiguity function of interest is a 2-dimensional
Dirac delta function or"thumbtack" function; that is, a function which is infinite at (0,0) andzero elsewhere.:
An ambiguity function of this kind would be somewhat of a misnomer; itwould have no ambiguities at all, and both the zero-delay and zero-Doppler cuts would be an impulse. However, any Doppler shift would make the target disappear. This is not desirable if a target has unknown velocity it will disappear from the radar picture, but if Dopplerprocessing is independently performed, knowledge of the preciseDoppler frequency allows ranging without interferencefrom any other targets which are not also moving at exactly the samevelocity.
This type of ambiguity function is not physically realizable; that is, there is no pulse that will produce from the definition of the ambiguity function. Approximations exist, however, and binary phase-shift keyed waveforms using maximal-length sequences are the best known performers in this regard [G. Jourdain and J. P. Henrioux, "Use of large bandwidth-duration binary phase shift keying signals in target delay Doppler measurements," J. Acoust. Soc. Am. 90, 299-309 (1991).] .
Properties of the ambiguity function
(1) Maximum value
:
(2) Symmetry about the origin
:
(3) Volume invariance
:
(4) Modulation
:If s(t) then (5) Frequency energy spectrum
:
Square Pulse
280px|thumb|right|Ambiguityfunction for a square pulseConsider a simple square pulse of duration andamplitude :
:
where is the
Heaviside step function . Thematched filter output is given by theautocorrelation of the pulse, which is a triangular pulse of height andduration (the zero-Doppler cut). However, if themeasured pulse has a frequency offset due to Doppler shift, thematched filter output is distorted into asinc function . Thegreater the Doppler shift, the smaller the peak of the resulting sinc,and the more difficult it is to detect the target.In general, the square pulse is not a desirable waveform from a pulse compression standpoint, because the autocorrelation function is too short in amplitude, making it difficult to detect targets in noise, and too wide in time, making it difficult to discern multiple overlapping targets.
LFM Pulse
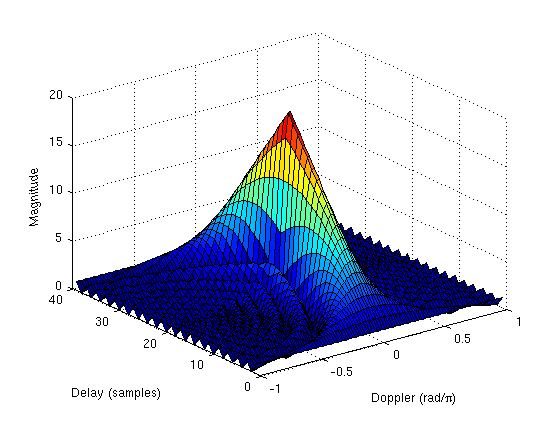
280px|thumb|right|Ambiguityfunction for an LFM pulseA commonly used
radar orsonar pulse is the linear frequency modulated (LFM)pulse (or "chirp"). It has the advantage of greater bandwidth whilekeeping the pulse duration short and envelope constant. A constant envelope LFM pulse has an ambiguity function similar to that of the square pulse, except that it is skewed in the delay-Doppler plane. Slight Dopplermismatches for the LFM pulse do not change the general shape of thepulse and reduce the amplitude very little, but they do appear to shift the pulsein time. Thus, an uncompensated Doppler shift changes the target's apparent range;this phenomenon is called range-Doppler coupling.References
*Richards, Mark A. "Fundamentals of Radar Signal Processing". McGraw-Hill Inc., 2005. ISBN 0-07-144474-2.
*Ipatov, Valery P. "Spread Spectrum and CDMA". Wiley & Sons, 2005. ISBN 0-470-09178-9
*Weiss, Lora G. "Wavelets and Wideband Correlation Processing". "IEEE Signal Processing Magazine", pp. 13-32, Jan 1994
*Woodward P.M. "Probability and Information Theory with Applications to Radar", Norwood, MA: Artech House, 1980.See also
*
Matched filter
*Pulse compression
*Pulse-Doppler radar
*Digital signal processing
Wikimedia Foundation. 2010.