Sylvester–Gallai theorem

The Sylvester–Gallai theorem asserts that given a finite number of points in the Euclidean plane, either

1. all the points are collinear; or
2. there is a line which contains exactly two of the points.

This claim was posed as a problem by J. J. Sylvester (1893). Kelly (1986) suggests that Sylvester may have been motivated by a related phenomenon in algebraic geometry, in which the inflection points of a cubic curve in the complex projective plane form a configuration of nine points and twelve lines in which each line determined by two of the points contains a third point. The Sylvester–Gallai theorem implies that it is impossible for all nine of these points to have real coordinates. Eberhard Melchior (1940) proved the projective dual of this theorem, (actually, of a slightly stronger result). Unaware of Melchior's proof, Paul Erdős (1943) again stated the conjecture, which was proved first by Tibor Gallai, and soon afterwards by other authors.^[1]

A line that contains exactly two of a set of points is known as an ordinary line. There is an algorithm that finds an ordinary line in a set of n points in time proportional to n log n in the worst case.^[2]

The Sylvester–Gallai theorem does not apply to sets of infinitely many points: all points in the plane or in the unit disk are obvious counterexamples. For countable counterexamples, consider for instance the lattice of integer points, or all rational points in the unit disc. As the example of the inflection points of a cubic curve shows, the Sylvester–Gallai theorem also does not apply to the complex projective plane.

Projective and dual versions

The question of the existence of an ordinary line can also be posed for points in the real projective plane RP² instead of the Euclidean plane. This provides no additional generality, as any finite set of projective points can be transformed into a Euclidean point set preserving all ordinary lines; but the projective viewpoint allows certain configurations to be described more easily.

By projective duality, the existence of an ordinary line in a set of non-collinear points in RP² is equivalent to the existence of an ordinary point in a nontrivial arrangement of finitely many lines. An arrangement is said to be trivial when all its lines pass through a common point, and nontrivial otherwise; an ordinary point is a point that belongs to exactly two lines.

Proofs

Kelly's proof

For a description of Gallai's original proof of the theorem, see e.g. Borwein & Moser (1990). The proof below is instead due to Kelly.

Suppose for contradiction that we have a finite set of points not all collinear but with at least three points on each line. Call it S. Define a connecting line to be a line which contains at least two points in the collection. Let (P,l) be the point and connecting line that are the smallest positive distance apart among all point-line pairs.

By the supposition, the connecting line l goes through at least three points of S, so dropping a perpendicular from P to l there must be at least two points on one side of the perpendicular (one might be exactly on the intersection of the perpendicular with l). Call the point closer to the perpendicular B, and the farther point C. Draw the line m connecting P to C. Then the distance from B to m is smaller than the distance from P to l, contradicting the original definition of P and l. One way to see this is to notice that the right triangle with hypotenuse BC is similar to and contained in the right triangle with hypotenuse PC.

Thus there cannot be a smallest positive distance between point-line pairs—every point must be distance 0 from every line. In other words, every point must lie on the same line if each connecting line has at least three points.

Melchior's proof

In 1940, therefore prior to Gallai's proof, Melchior showed that any nontrivial finite arrangement of lines in the projective plane has at least three ordinary points. By duality, this results also says that any finite nontrvial set of points on the plane has at least three ordinary lines.

Melchior observed that, for any graph embedded in RP², the formula V − E + F must equal 1, the Euler characteristic of RP²; where V, E, and F, are the number of vertices, edges, and faces of the graph, respectively. Any nontrivial line arrangement on RP² defines a graph in which each face is bounded by at least three edges, and each edge bounds two faces; so, double counting gives the additional inequality F ≤ 2E/3. Using this inequality to eliminate F from the Euler characteristic leads to the inequality E ≤ 3V − 3. But if every vertex in the arrangement were the crossing point of three or more lines, then the total number of edges would be at least 3V, contradicting this inequality. Therefore, some vertices must be the crossing point of only two lines, and as Melchior's more careful analysis shows, at least three ordinary vertices are needed in order to satisfy the inequality E ≤ 3V − 3.

Melchior's inequality

By a similar argument, Melchior was able to prove a more general result. For every k ≥ 2, let t_k be the number of points to which k lines are incident. Then

$\displaystyle \sum_{k\geq2} (k-3) t_k \leq -3.\,\!$

Equivalently,

$\displaystyle t_2 \geqslant 3 + \sum_{k\geq4} (k-3) t_k.\,\!$

This is often referred to as Melchior's inequality.

Coxeter's proof

H. S. M. Coxeter (1969) gave another proof of the Sylvester–Gallai theorem within ordered geometry, an axiomatization of geometry that includes not only Euclidean geometry but several other related geometries. See Pambuccian (2009) for minimal axiom systems inside which the Sylvester–Gallai theorem can be proved.

The number of ordinary lines

The two known examples of point sets with fewer than n/2 ordinary lines.

While the Sylvester–Gallai theorem tells us that an arrangement of points, not all collinear, must determine an ordinary line, it does not say how many must be determined.

Let t₂(n) be the minimum number of ordinary lines determined over every set of n non-collinear points. Melchior's proof showed that t₂(n) ≥ 3. de Bruijn and Erdős (1948) raised the question of whether t₂(n) approaches infinity with n. Theodore Motzkin (1951) confirmed this conjecture by proving that t₂(n) ≥ √n. Gabriel Dirac (1951) conjectured that t₂(n) ≥ ⌊n/2⌋ for all values of n, a conjecture that still stands as of 2011^[update]. This is often referred to as the Dirac-Motzkin conjecture, see for example Brass, Moser & Pach (2005, p. 304). Kelly & Moser (1958) proved that t₂(n) ≥ 3n/7.

Dirac's conjectured lower bound is asymptotically the best possible, since there is a proven matching upper bound t₂(n) ≤ n/2 for even n greater than four.^[3]

Example of Böröczky's (even) configuration with 10 points determining 5 ordinary lines.

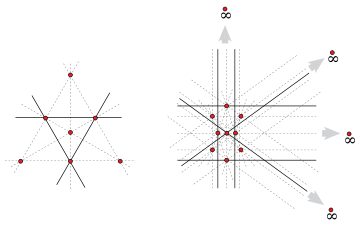
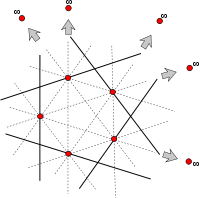
The construction, due to Károly Böröczky, that achieves this bound consists of the vertices of a regular m-gon in the real projective plane and another m points (thus, n = 2m) on the line at infinity corresponding to each of the directions determined by pairs of vertices; although there are m(m − 1)/2 pairs, they determine only m distinct directions. This arrangement has only m ordinary lines, namely those that connect a vertex v with the point at infinity corresponding to the line determined by v's two neighboring vertices. Note that, as with any finite configuration in the real projective plane, this construction can be perturbed so that all points are finite, without changing the number of ordinary lines.

For odd n, only two examples are known that match Dirac's lower bound conjecture, that is, with t₂(n) = (n − 1)/2. One example, by Kelly & Moser (1958), consists of the vertices, edge midpoints, and centroid of an equilateral triangle; these seven points determine only three ordinary lines. The configuration in which these three ordinary lines are replaced by a single line cannot be realized in the Euclidean plane, but forms a finite projective space known as the Fano plane. The other counterexample, due to McKee,^[3] consists of two regular pentagons joined edge-to-edge together with the midpoint of the shared edge and four points on the line at infinity in the projective plane; these 13 points have among them 6 ordinary lines.

As of 2009^[update], the best proven lower bound for t₂(n) was obtained by Csima & Sawyer (1993) who proved that t₂(n) ≥ ⌈6n/13⌉ except when n is seven. Asymptotically, this formula is already 12/13 ~ 92.3% of the proven n/2 upper bound. The n = 7 case is an exception because otherwise the Kelly–Moser construction would be a counterexample; their construction shows that t₂(7) ≤ 3. However, were the Csima–Sawyer bound valid for n = 7, it would claim that t₂(7) ≥ 4.

A closely related result is Beck's theorem, stating a tradeoff between the number of lines with few points and the number of points on a single line.

See also

• Sylvester's theorem (disambiguation page)
• List of topics named after James Joseph Sylvester
• The de Bruijn–Erdős theorem, a consequence of this theorem, states that a set of n noncollinear points determines n lines.
• Orchard-planting problem

Notes

1. ^ Steinberg et al. (1944); Erdős (1982).
2. ^ Mukhopadhyay, Agrawal & Hosabettu (1997); Mukhopadhyay & Greene (2007).
3. ^ ^{a b} Crowe & McKee (1968).

References

• Borwein, P.; Moser, W. O. J. (1990), "A survey of Sylvester's problem and its generalizations", Aequationes Mathematicae 40 (1): 111–135, doi:10.1007/BF02112289 .
• Brass, Peter; Moser, William; Pach, János (2005), Research problems in discrete geometry, Berlin: Springer, ISBN 0-387-23815-8 .
• de Bruijn, N. G.; Erdős, P. (1948), "A combinatioral [sic] problem", Indagationes Mathematicae 10: 421–423, http://www.renyi.hu/~p_erdos/1948-01.pdf .
• Coxeter, H. S. M. (1969), Introduction to Geometry, New York: John Wiley & Sons, pp. 181–182, ISBN 0471504580 .
• Crowe, D. W.; McKee, T. A. (1968), "Sylvester's problem on collinear points", Mathematics Magazine 41 (1): 30–34, doi:10.2307/2687957, JSTOR 2687957 .
• Csima, J.; Sawyer, E. (1993), "There exist 6n/13 ordinary points", Discrete & Computational Geometry 9: 187–202, doi:10.1007/BF02189318 .
• Dirac, G. (1951), "Collinearity properties of sets of points", Quart. J. Math. 2: 221–227, doi:10.1093/qmath/2.1.221 .
• Erdős, P.; Bellman, Richard; Wall, H. S; Singer, James; Thébault, V (1943), Problem 4065, "Problems for solution: 4065–4069", American Mathematical Monthly 50 (1): 65–66, doi:10.2307/2304011, JSTOR 2304011 .
• Erdős, P. (1982), "Personal reminiscences and remarks on the mathematical work of Tibor Gallai", Combinatorica 2 (3): 207–212, doi:10.1007/BF02579228, http://www.math-inst.hu/~p_erdos/1982-22.pdf .
• Kelly, L. M. (1986), "A resolution of the Sylvester–Gallai problem of J. P. Serre", Discrete and Computational Geometry 1 (1): 101–104, doi:10.1007/BF02187687 .
• Kelly, L. M.; Moser, W. O. J. (1958), "On the number of ordinary lines determined by n points", Canad. J. Math. 10: 210–219, doi:10.4153/CJM-1958-024-6, http://www.cms.math.ca/cjm/v10/p210 .
• Melchior, E. (1940), "Über Vielseite der Projektive Ebene", Deutsche Math. 5: 461–475 .
• Motzkin, Th. (1951), "The lines and planes connecting the points of a finite set", Transactions of the American Mathematical Society. 70 (3): 451–464, doi:10.2307/1990609, JSTOR 1990609 .
• Mukhopadhyay, A.; Agrawal, A.; Hosabettu, R. M. (1997), "On the ordinary line problem in computational geometry", Nordic Journal of Computing 4 (4): 330–341 .
• Mukhopadhyay, A.; Greene, E. (2007), "The ordinary line problem revisited", Proc. 19th Canadian Conference on Computational Geometry, pp. 61–64, http://cccg.ca/proceedings/2007/03a4.pdf .
• Pambuccian, V. (2009), "A reverse analysis of the Sylvester-Gallai theorem", Notre Dame Journal of Formal Logic. 50 (3): 245–260, doi:10.1215/00294527-2009-010, http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.ndjfl/1257862037 .
• Steinberg, R.; Buck, R. C.; Grünwald, T.; Steenrod, N. E. (1944), "Three point collinearity (solution to problem 4065)", American Mathematical Monthly 51 (3): 169–171, doi:10.2307/2303021, JSTOR 2303021 .
• Sylvester, J. J. (1893), "Mathematical question 11851", Educational Times 59: 98 .

External links

• Malkevitch, Joseph (2003). "A discrete geometrical gem". http://e-math.ams.org/featurecolumn/archive/sylvester1.html. 
• Weisstein, Eric W., "Ordinary Line" from MathWorld.