Oscillator Toda

Oscillator Toda is special kind of nonlinear oscillator; it is vulgarization of the Toda field theory, which refers to a continuous limit of Toda's chain, of chain of particles, with exponential potential of interaction between neighbors cite journal| author=M.Toda|title=Studies of a non-linear lattice|journal=Physics Reports|volume=18|pages=1|year=1975|doi=10.1016/0370-1573(75)90018-6] . The oscillator Toda is used as simple model to understand the phenomenon of self-pulsation, which is quasi-periodic pulsation of the output intensity of a solid-state lasers in the transient regime.

Definition

Oscillator Toda is a dynamical system of any origin, which can be described with dependent coordinate $~x~$ and independent coordinate $~z~$, characterized in that the evolution along independent coordinate $~z~$ can be approximated with equation: $frac$ m d^{2x} m d}z^{2+D(x)frac m d}x} m d}z}+Phi'(x) =0,where $~D(x)=u\; e^\{x\}+v~$,$~Phi(x)=e^x-x-1~$and prime denotes the derivative.

Physical meaning

The independent coordinate $~z~$ has sense of time. Indeed, it may be proportional to time $~t~$ with some relation like $~z=t/t\_0~$, where $~t\_0~$ is constant.

The derivative $~dot\; x=frac$ m d}x} m d}z} may have sense of velocity of particle with coordinate $~x~$; then $~ddot\; x=frac$ m d}^2x} m d}z^2}~ can be interpreted as acceleration; and the mass of such a particle is equal to unity.

The dissipative function $~D~$ may have sense of coefficient of the speed-proportional friction. Usually, both parameters $~u~$ and $~v~$ are supposed to be positive; then this speed-proportional friction coefficient grows exponentially at large positive values of coordinate $~x~$.

The potential $~Phi(x)=e^x-x-1~$ is fixed function, which also shows exponential grow at large positive values of coordinate $~x~$.

In the application in laser physics, $~x~$ may have sense of logarithm of number of photons in the laser cavity, related to its steady-state value. Then, the output power of such laser is proportional to $~exp(x)~$ and may show pulsation at oscillation of $~x~$.

Both analogies, with a unity mass particle and logarithm of number of photons are useful in the analysis of behavior of oscillator Toda.

Energy

Rigorously, the oscillation is periodic only at $~u=v=0~$. Indeed in realization of oscillator Toda as self-pulsing laser,these parameters may have values of order of $~10^\{-4\}~$; during several pulses, the amplutude of pulsation does not change much. In this case, we can speak about period of pulsation, function $~x=x(t)~$ is almost periodic.

In the case $~u=v=0~$, the energy of oscillator $~E=frac\; 12\; left(frac$ m d}x} m d}z} ight)^{2}+Phi(x)~ does not depend on $~z~$, and can be treated as constant of motion. Then, during one period of pulsation, the relation between $~x~$ and $~z~$ can be expressed analyticallycite journal|url=http://worldcat.org/issn/0722-3277| author=G.L.Oppo|coauthors=A.Politi|title=Toda potential in laser equations|journal=Zeitschrift fur Physik B|volume=59|pages=111–115| year=1985|doi=10.1007/BF01325388] ,cite journal|url=http://www.iop.org/EJ/abstract/-search=15823442.1/1751-8121/40/9/016| author=D.Kouznetsov|coauthors=J.-F.Bisson, J.Li, K.Ueda|title=Self-pulsing laser as oscillator Toda: Approximation through elementary functions|journal=Journal of Physics A|volume=40|pages=1–18| year=2007|doi=10.1088/1751-8113/40/9/016] :

:$z=pmint\_\{x\}^\{x\_\{max$!!frac m d}a}{sqrt{2}sqrt{E-Phi(a)

wehere$~x\_\{min\}~$ and $~x\_\{max\}~$ are minimal and maximal values of $~x~$; this solution is written for the case when $dot\; x(0)=0$.

however, other solutions may be obtained using the translational invariance.

---

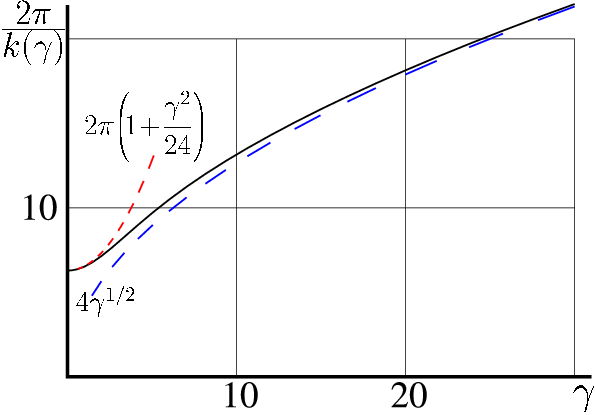
right|300px|thumb|Fig.2. Period ">$~T(gamma)=2pi/k(gamma)~$ of oscillation versus $~gamma~$(solid) and two its asymptiotics (dashed).The ratio $~x\_\{max\}/x\_\{max\}=2gamma~$ is convenient parameter to characterize the amplitude of pulsation,then, the median value$delta=frac\{x\_max\; -x\_min\}\{1\}$can be expressed as$delta=lnfrac\{sin(gamma)\}\{gamma\}$;and the energy$E=E(gamma)=frac\{gamma\}\{\; anh(gamma)\}+lnfrac\{sinh\; gamma\}\{gamma\}-1$also is elementary function of $~gamma~$.For the case $~gamma=5~$, an example of pulsation of the oscillator toda is shown in Fig.1.

In application, the quantity $E$ have no need to be physical energy of the system; in these cases, this dimension-less quantity may be called quasienergy.

Period of pulsation

The period of pulsation is increasing function of the amplitude $~gamma~$.

At $~gamma\; ll\; 1~$, the period $~T(gamma)=2pileft(\; 1\; +\; frac\{gamma^2\}\; \{24\}\; +\; O(gamma^4)\; ight)~$

At $~gamma\; gg\; 1~$, the period $~T(gamma)=4gamma^\{1/2\}left(1+O(1/gamma)\; ight)\; ~$

In the whole range$~gamma\; >\; 0~$, the period $~T=T(gamma)~$ and the frequency $~k(gamma)=frac\{2pi\}\{T(gamma)\}~$ can be approximated with

$k\_\{\; m\; fit\}(gamma)=frac\{2pi\}\{T\_\{\; m\; fit\}(gamma)\}=$$left(frac\{10630+\; 674gamma\; +\; 695.2419gamma^2\; +\; 191.4489gamma^3\; +\; 16.86221gamma^4\; +\; 4.082607gamma^5\; +\; gamma^6\}\{10630\; +\; 674gamma\; +\; 2467gamma^2\; +\; 303.2428\; gamma^3+164.6842gamma^4\; +\; 36.6434gamma^5\; +\; 3.9596gamma^6\; +0.8983gamma^7\; +frac\{16\}\{pi^4\}\; gamma^8\}\; ight)^\{1/4\}$with at least 8 significant figures;The relative error of this approximation does not exceed $22\; imes\; 10^\{-9\}$.

Decay of pulsation

At small (but still positive) values of $~u~$ and $~v~$, the pulsation decays slowly, and this decay can be described analytically. In the first approximation parameters $~u~$ and $~v~$ hive additive contribution to the decay; the decay rate, as well as the amplitude and phase of the nonlinear oscillation can be approximated with elementary functions in the similar manner, as the period above. This allows to approximate the solution of the initial equation; and the error of such approximation is small compared to the difference between behavior of the idealized oscillator Toda and behavior of the experimental realization of oscillator Toda as self-pulsing laser at the optical bench, although, qualitatively, a self-pulsing laser shows very similar behavior.cite journal|url=http://www.iop.org/EJ/abstract/-search=15823442.1/1751-8121/40/9/016| author=D.Kouznetsov|coauthors=J.-F.Bisson, J.Li, K.Ueda|title=Self-pulsing laser as oscillator Toda: Approximation through elementary functions|journal=Journal of Physics A|volume=40|pages=1–18| year=2007|doi=10.1088/1751-8113/40/9/016]

References