Disk covering problem

The disk covering problem was proposed by C. T. Zahn in 1962.

Given an integer n, the problem asks for the smallest real number r(n) such that n disks of radius r(n) can be arranged in such a way as to cover the unit disk.

The best solutions to date are as follows:

n	r(n)
1	1
2	1
3	1 / 2 * sqrt(3)
4	1 / 2 * sqrt(2)
5	0.609382...
6	0.555905...
7	1 / 2
8	0.445041...
9	0.414213... 1 / 2 * sqrt(3)
10	0.394930...

Method

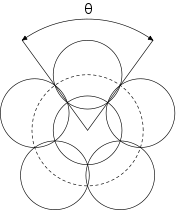
This is the best know layout strategy for r(9) and r(10):

External links

• Weisstein, Eric W. "Disk Covering Problem." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/DiskCoveringProblem.html
• Finch, S. R. "Circular Coverage Constants." §2.2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 484-489, 2003.
• Illustrations of circles covering circles

This geometry-related article is a stub. You can help Wikipedia by expanding it.v · Categories: Geometry stubs Discrete geometry Mathematical problems Wikimedia Foundation. 2010. Игры ⚽ Поможем написать курсовую Zeta Phi Thomas Stanage Look at other dictionaries: Covering problem of Rado — The covering problem of Rado is an unsolved problem in geometry concerning covering planar sets by squares. It was formulated in 1928 by Tibor Radó and has been generalized to more general shapes and higher dimensions by Richard Rado. Formulation …   Wikipedia Disk encryption — uses disk encryption software or hardware to encrypt every bit of data that goes on a disk or disk volume. Disk encryption prevents unauthorized access to data storage. The term full disk encryption (or whole disk encryption) is often used to… …   Wikipedia Nipkow disk — Schematic showing the circular paths traced by the holes in a Nipkow disk A Nipkow disk (sometimes Anglicized as Nipkov disk), also known as scanning disk, is a mechanical, geometrically operating image scanning device, invented by Paul Gottlieb… …   Wikipedia Year 2000 problem — Y2K redirects here. For other uses, see Y2K (disambiguation). The (French) sign reads 3 January 1900 instead of 3 January 2000 The Year 2000 problem (also known as the Y2K problem, the Millennium bug, the Y2K bug, or simply Y2K) was a problem for …   Wikipedia List of mathematics articles (D) — NOTOC D D distribution D module D D Agostino s K squared test D Alembert Euler condition D Alembert operator D Alembert s formula D Alembert s paradox D Alembert s principle Dagger category Dagger compact category Dagger symmetric monoidal… …   Wikipedia combinatorics — /keuhm buy neuh tawr iks, tor , kom beuh /, n. (used with singular v.) See combinatorial analysis. * * * Branch of mathematics concerned with the selection, arrangement, and combination of objects chosen from a finite set. The number of possible… …   Universalium Color television — Title card for NBC, promoting their broadcast in RCA color . Color television is part of the history of television, the technology of television and practices associated with television s transmission of moving images in color video. In its most… …   Wikipedia Apple File Exchange — is a utility included on the Tidbits disk or Install 2 disk in system versions 7.0 through 7.1. In System 7.5, it was replaced by PC Exchange.Apple File Exchange could read floppy disks from Macs, as well as disks from DOS/Windows and ProDOS… …   Wikipedia Quantitative comparative linguistics — is a branch of comparative linguistics that applies mathematical models to the problem of classifying language relatedness. This includes the use of computational phylogenetics and cladistics to define an optimal tree (or network) to represent a… …   Wikipedia pre-Columbian civilizations — Introduction       the aboriginal American Indian (Mesoamerican Indian) cultures that evolved in Meso America (part of Mexico and Central America) and the Andean region (western South America) prior to Spanish exploration and conquest in the 16th …   Universalium 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”