- Reaction–diffusion system
-
Reaction–diffusion systems are mathematical models which explain how the concentration of one or more substances distributed in space changes under the influence of two processes: local chemical reactions in which the substances are transformed into each other, and diffusion which causes the substances to spread out over a surface in space.
This description implies that reaction–diffusion systems are naturally applied in chemistry. However, the system can also describe dynamical processes of non-chemical nature. Examples are found in biology, geology and physics and ecology. Mathematically, reaction–diffusion systems take the form of semi-linear parabolic partial differential equations. They can be represented in the general form
where each component of the vector q(x,t) represents the concentration of one substance, D is a diagonal matrix of diffusion coefficients, and R accounts for all local reactions. The solutions of reaction–diffusion equations display a wide range of behaviours, including the formation of travelling waves and wave-like phenomena as well as other self-organized patterns like stripes, hexagons or more intricate structure like dissipative solitons.
Contents
One-component reaction–diffusion equations
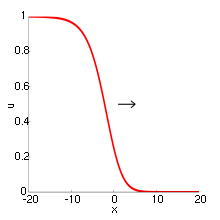
The most simple reaction–diffusion equation concerning the concentration u of a single substance in one spatial dimension,
is also referred to as the KPP (Kolmogorov-Petrovsky-Piskounov) equation. [1] If the reaction term vanishes, then the equation represents a pure diffusion process. The corresponding equation is Fick's second law. The choice R(u) = u(1-u) yields Fisher's equation that was originally used to describe the spreading of biological populations, [2] the Newell-Whitehead-Segel equation with R(u) = u(1 − u2) to describe Rayleigh-Benard convection, [3][4] the more general Zeldovich equation with R(u) = u(1 − u)(u − α) and 0 < α < 1 that arises in combustion theory, [5] and its particular degenerate case with R(u) = u2 − u3 that is sometimes referred to as the Zeldovich equation as well. [6]
The dynamics of one-component systems is subject to certain restrictions as the evolution equation can also be written in the variational form
and therefore describes a permanent decrease of the "free energy"
 given by the functional
given by the functionalwith a potential V(u) such that R(u)=dV(u)/du.
In systems with more than one stationary homogeneous solution, a typical solution is given by travelling fronts connecting the homogeneous states. These solutions move with constant speed without changing their shape and are of the form u(x, t) = û(ξ) with ξ = x − ct, where c is the speed of the travelling wave. Note that while travelling waves are generically stable structures, all non-monotonous stationary solutions (e.g. localized domains composed of a front-antifront pair) are unstable. For c = 0, there is a simple proof for this statement:[7] if u0(x) is a stationary solution and u=u0(x) + ũ(x, t) is an infinitesimally perturbed solution, linear stability analysis yields the equation
With the ansatz ũ = ψ(x)exp(−λt) we arrive at the eigenvalue problem
of Schrödinger type where negative eigenvalues result in the instability of the solution. Due to translational invariance ψ = ∂xu0(x) is a neutral eigenfunction with the eigenvalue λ = 0, and all other eigenfunctions can be sorted according to an increasing number of knots with the magnitude of the corresponding real eigenvalue increases monotonically with the number of zeros. The eigenfunction ψ = ∂x u0(x) should have at least one zero, and for a non-monotonic stationary solution the corresponding eigenvalue λ = 0 cannot be the lowest one, thereby implying instability.
To determine the velocity c of a moving front, one may go to a moving coordinate system and look at stationary solutions:
This equation has a nice mechanical analogue as the motion of a mass D with position û in the course of the "time" ξ under the force R with the damping coefficient c which allows for a rather illustrative access to the construction of different types of solutions and the determination of c.
When going from one to more space dimensions, a number of statements from one-dimensional systems can still be applied. Planar or curved wave fronts are typical structures, and a new effect arises as the local velocity of a curved front becomes dependent on the local radius of curvature (this can be seen by going to polar coordinates). This phenomenon leads to the so-called curvature-driven instability.[8]
Two-component reaction–diffusion equations
Two-component systems allow for a much larger range of possible phenomena than their one-component counterparts. An important idea that was first proposed by Alan Turing is that a state that is stable in the local system should become unstable in the presence of diffusion. [9] This idea seems unintuitive at first glance as diffusion is commonly associated with a stabilizing effect.
A linear stability analysis however shows that when linearizing the general two-component system
a plane wave perturbation
of the stationary homogeneous solution will satisfy
Turing's idea can only be realized in four equivalence classes of systems characterized by the signs of the Jacobian R' of the reaction function. In particular, if a finite wave vector k is supposed to be the most unstable one, the Jacobian must have the signs
This class of systems is named activator-inhibitor system after its first representative: close to the ground state, one component stimulates the production of both components while the other one inhibits their growth. Its most prominent representative is the FitzHugh–Nagumo equation
with ƒ(u) = λu − u3 − κ which describes how an action potential travels through a nerve. [10][11] Here, du, dv, τ, σ and λ are positive constants.
When an activator-inhibitor system undergoes a change of parameters, one may pass from conditions under which a homogeneous ground state is stable to conditions under which it is linearly unstable. The corresponding bifurcation may be either a Hopf bifurcation to a globally oscillating homogeneous state with a dominant wave number k = 0 or a Turing bifurcation to a globally patterned state with a dominant finite wave number. The latter in two spatial dimensions typically leads to stripe or hexagonal patterns.
- Subcritical Turing bifurcation: formation of a hexagonal pattern from noisy initial conditions in the above two-component reaction-diffusion system of Fitzhugh-Nagumo type.
-

Noisy initial conditions at t = 0.
-

State of the system at t = 10.
-

Almost converged state at t = 100.
For the Fitzhugh-Nagumo example, the neutral stability curves marking the boundary of the linearly stable region for the Turing and Hopf bifurcation are given by
If the bifurcation is subcritical, often localized structures (dissipative solitons) can be observed in the hysteretic region where the pattern coexists with the ground state. Other frequently encountered structures comprise pulse trains, spiral waves and target patterns.
- Other patterns found in the above two-component reaction-diffusion system of Fitzhugh-Nagumo type.
-

Rotating spiral.
-

Target pattern.
-

Stationary localized pulse (dissipative soliton).
Three- and more-component reaction–diffusion equations
For a variety of systems, reaction-diffusion equations with more than two components have been proposed, e.g. as models for the Belousov-Zhabotinsky reaction, [12], for blood clotting[13] or planar gas discharge systems. [14]
While it is known that systems with more components allow for a variety of phenomena not possible in systems with one or two components (e.g. stable running pulses in more than one spatial dimension without global feedback)[15], up to now a systematic overview of the possible phenomena in dependence on the properties of the underlying system is hardly present.
Applications and universality
In recent times, reaction–diffusion systems have attracted much interest as a prototype model for pattern formation. The above-mentioned patterns (fronts, spirals, targets, hexagons, stripes and dissipative solitons) can be found in various types of reaction-diffusion systems in spite of large discrepancies e.g. in the local reaction terms. It has also been argued that reaction-diffusion processes are an essential basis for processes connected to morphogenesis in biology[16] and may even be related to animal coats and skin pigmentation.[17][18]
See also: The chemical basis of morphogenesisAnother reason for the interest in reaction-diffusion systems is that although they represent nonlinear partial differential equation, there are often possibilities for an analytical treatment.[7][8][19][20][21]
Experiments
Well-controllable experiments in chemical reaction-diffusion systems have up to now been realized in three ways. First, gel reactors[22] or filled capillary tubes[23] may be used. Second, temperature pulses on catalytic surfaces have been investigated.[24][25] Third, the propagation of running nerve pulses is modelled using reaction-diffusion systems.[10][26]
Aside from these generic examples, it has turned out that under appropriate circumstances electric transport systems like plasmas[27] or semiconductors[28] can be described in a reaction-diffusion approach. For these systems various experiments on pattern formation have been carried out.
See also
- Diffusion-controlled reaction
- Chemical kinetics
- Phase space method
- Fisher's equation
- Autocatalytic reactions and order creation
- Pattern formation
- Stochastic geometry
- MClone
References
- ^ A. Kolmogorov et al., Moscow Univ. Bull. Math. A 1 (1937): 1
- ^ R. A. Fisher, Ann. Eug. 7 (1937): 355
- ^ A. C. Newell and J. A. Whitehead, J. Fluid Mech. 38 (1969): 279
- ^ L. A. Segel, J. Fluid Mech. 38 (1969): 203
- ^ Y. B. Zeldovich and D. A. Frank-Kamenetsky, Acta Physicochim. 9 (1938): 341
- ^ B. H. Gilding and R. Kersner, Travelling Waves in Nonlinear Diffusion Convection Reaction, Birkhäuser (2004)
- ^ a b P. C. Fife, Mathematical Aspects of Reacting and Diffusing Systems, Springer (1979)
- ^ a b A. S. Mikhailov, Foundations of Synergetics I. Distributed Active Systems, Springer (1990)
- ^ A. M. Turing, Phil. Transact. Royal Soc. B 237 (1952): 37
- ^ a b R. FitzHugh, Biophys. J. 1 (1961): 445
- ^ J. Nagumo et al., Proc. Inst. Radio Engin. Electr. 50 (1962): 2061
- ^ V. K. Vanag and I. R. Epstein, Phys. Rev. Lett. 92 (2004): 128301
- ^ E. S. Lobanova and F. I. Ataullakhanov, Phys. Rev. Lett. 93 (2004): 098303
- ^ H.-G. Purwins et al. in: Dissipative Solitons, Lectures Notes in Physics, Ed. N. Akhmediev and A. Ankiewicz, Springer (2005)
- ^ C. P. Schenk et al., Phys. Rev. Lett. 78 (1997): 3781
- ^ L.G. Harrison, Kinetic Theory of Living Pattern, Cambridge University Press (1993)
- ^ H. Meinhardt, Models of Biological Pattern Formation, Academic Press (1982)
- ^ J. D. Murray, Mathematical Biology, Springer (1993)
- ^ P. Grindrod,Patterns and Waves: The Theory and Applications of Reaction-Diffusion Equations, Clarendon Press (1991)
- ^ J. Smoller, Shock Waves and Reaction Diffusion Equations, Springer (1994)
- ^ B. S. Kerner and V. V. Osipov, Autosolitons. A New Approach to Problems of Self-Organization and Turbulence, Kluwer Academic Publishers (1994)
- ^ K.-J. Lee et al., Nature 369 (1994): 215
- ^ C. T. Hamik and O. Steinbock, New J. Phys. 5 (2003): 58
- ^ H. H. Rotermund et al., Phys. Rev. Lett. 66 (1991): 3083
- ^ M. D. Graham et al., J. Phys. Chem. 97 (1993): 7564
- ^ A. L. Hodgkin and A. F. Huxley, J. Physiol. 117 (1952): 500
- ^ M. Bode and H.-G. Purwins, Physica D 86 (1995): 53
- ^ E. Schöll, Nonlinear Spatio-Temporal Dynamics and Chaos in Semiconductors, Cambridge University Press (2001)
External links
- Java applet showing a reaction–diffusion simulation
- Another applet showing Gray-Scott reaction-diffusion.
- Gallery of reaction-diffusion images and movies.
- TexRD software random texture generator based on reaction-diffusion for graphists and scientific use
- Reaction-Diffusion by the Gray-Scott Model: Pearson's parameterization a visual map of the parameter space of Gray-Scott reaction diffusion.
- A Thesis on reaction-diffusion patterns with an overview of the field
Categories:- Mathematical modeling
- Parabolic partial differential equations
Wikimedia Foundation. 2010.




![\mathfrak L=\int\limits_{-\infty}^\infty\left[\frac
D2(\partial_xu)^2-V(u)\right]\text{d}x](a/01a3574059d7401fe26c6e5a4c8a6df3.png)








![\begin{align}
q_{\text{n}}^H(k): &{}\quad \frac{1}{\tau} + (d_u^2 + \frac{1}{\tau} d_v^2)k^2 & =f^{\prime}(u_{h}),\\[6pt]
q_{\text{n}}^T(k): &{}\quad \frac{\kappa_3}{1 + d_v^2 k^2}+ d_u^2 k^2 & = f^{\prime}(u_{h}).
\end{align}](d/b9daf9a4a83290a65fa189dbcaf2f970.png)