Dehn twist

A positive Dehn twist applied to a cylinder about the red curve c modifies the green curve as shown.

In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface (two-dimensional manifold).

Definition

Suppose that c is a simple closed curve in a closed, orientable surface S. Let A be a tubular neighborhood of c. Then A is an annulus and so is homeomorphic to the Cartesian product of

$S^1 \times I,$

where I is the unit interval. Give A coordinates (s, t) where s is a complex number of the form

e^iθ

with

$\theta \in [0,2\pi],$

and t in the unit interval.

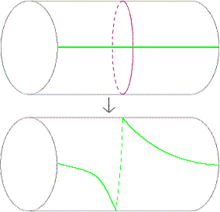
Let f be the map from S to itself which is the identity outside of A and inside A we have

$\displaystyle f(s,t) = (s e^{{\rm{i}} 2 \pi t}, t).$

Then f is a Dehn twist about the curve c.

Dehn twists can also be defined on a non-orientable surface S, provided one starts with a 2-sided simple closed curve c on S.

Mapping class group

The 3g − 1 curves from the twist theorem, shown here for g = 3.

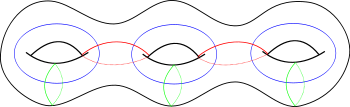
It is a theorem of Max Dehn that maps of this form generate the mapping class group of isotopy classes of orientation-preserving homeomorphisms of any closed, oriented genus-g surface. W. B. R. Lickorish later rediscovered this result with a simpler proof and in addition showed that Dehn twists along 3g − 1 explicit curves generate the mapping class group (this is called by the punning name "Lickorish twist theorem"); this number was later improved by Stephen P. Humphries to 2g + 1, for g > 1, which he showed was the minimal number.

Lickorish also obtained an analogous result for non-orientable surfaces, which require not only Dehn twists, but also "Y-homeomorphisms."

See also

• Lantern relation

References

• Andrew J. Casson, Steven A Bleiler, Automorphisms of Surfaces After Nielsen and Thurston, Cambridge University Press, 1988. ISBN 0-521-34985-0.
• Stephen P. Humphries, Generators for the mapping class group, in: Topology of low-dimensional manifolds (Proc. Second Sussex Conf., Chelwood Gate, 1977), pp. 44–47, Lecture Notes in Math., 722, Springer, Berlin, 1979. MR0547453
• W. B. R. Lickorish, A representation of orientable combinatorial 3-manifolds. Ann. of Math. (2) 76 1962 531—540. MR0151948
• W. B. R. Lickorish, A finite set of generators for the homeotopy group of a 2-manifold, Proc. Cambridge Philos. Soc. 60 (1964), 769–778. MR0171269