Motion field

In computer vision the motion field is an ideal representation of 3D motion as it is projected onto a camera image. Given a simplified camera model, each point (y₁,y₂) in the image is the projection of some point in the 3D scene but the position of the projection of a fixed point in space can vary with time. The motion field can formally be defined as the time derivative of the image position of all image points given that they correspond to fixed 3D points. This means that the motion field can be represented as a function which maps image coordinates to a 2-dimensional vector. The motion field is an ideal description of the projected 3D motion in the sense that it can be formally defined but in practice it is normally only possible to determine an approximation of the motion field from the image data.

Introduction

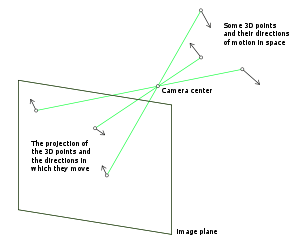An illustration of some 3D points and their corresponding image points as described by the pinhole camera model. As the 3D points are moving in space, the corresponding image points are also moving. The motion field consists of the motion vectors in the image for all points in the image.

A simple camera model implies that each point (x₁,x₂,x₃) in 3D space is projected to a 2D image point (y₁,y₂) according to some mapping functions m₁,m₂:

$\begin{pmatrix} y_{1} \\ y_{2} \end{pmatrix} = \begin{pmatrix} m_{1}(x_{1}, x_{2}, x_{3}) \\ m_{2}(x_{1}, x_{2}, x_{3}) \end{pmatrix}$

Assuming that the scene depicted by the camera is dynamic; it consists of objects moving relative each other, objects which deform, and possibly also the camera is moving relative to the scene, a fixed point in 3D space is mapped to varying points in the image. Differentiating the previous expression with respect to time gives

$\begin{pmatrix} \frac{d y_{1}}{d t} \\[2mm] \frac{d y_{2}}{d t} \end{pmatrix} = \begin{pmatrix} \frac{d m_{1}(x_{1}, x_{2}, x_{3})}{d t} \\[2mm] \frac{d m_{2}(x_{1}, x_{2}, x_{3})}{d t} \end{pmatrix} = \begin{pmatrix} \frac{d m_{1}}{d x_{1}} & \frac{d m_{1}}{d x_{2}} & \frac{d m_{1}}{d x_{3}} \\[2mm] \frac{d m_{2}}{d x_{1}} & \frac{d m_{2}}{d x_{2}} & \frac{d m_{2}}{d x_{3}} \end{pmatrix} \, \begin{pmatrix} \frac{d x_{1}}{d t} \\[2mm] \frac{d x_{2}}{d t} \\[2mm] \frac{d x_{3}}{d t} \end{pmatrix}$

Here

$\mathbf{u} = \begin{pmatrix} \frac{d y_{1}}{d t} \\[2mm] \frac{d y_{2}}{d t} \end{pmatrix}$

is the motion field and the vector u is dependent both on the image position (y₁,y₂) as well as on the time t. Similarly,

$\mathbf{x'} = \begin{pmatrix} \frac{d x_{1}}{d t} \\[2mm] \frac{d x_{2}}{d t} \\[2mm] \frac{d x_{3}}{d t} \end{pmatrix}$

is the motion of the corresponding 3D point and its relation to the motion field is given by

$\mathbf{u} = \mathbf{M} \, \mathbf{x}'$

where $\mathbf{M}$ is the image position dependent $2 \times 3$ matrix

$\mathbf{M} = \begin{pmatrix} \frac{d m_{1}}{d x_{1}} & \frac{d m_{1}}{d x_{2}} & \frac{d m_{1}}{d x_{3}} \\[2mm] \frac{d m_{2}}{d x_{1}} & \frac{d m_{2}}{d x_{2}} & \frac{d m_{2}}{d x_{3}} \end{pmatrix}$

This relation implies that the motion field, at a specific image point, is invariant to 3D motions which lies in the null space of $\mathbf{M}$. For example, in the case of a pinhole camera all 3D motion components which are directed to or from the camera focal point cannot be detected in the motion field.

Special cases

The motion field $\mathbf{v}$ is defined as:

$\mathbf{v} = f\frac{Z\mathbf{V} - V_z\mathbf{P}}{Z^2}$

where

$\mathbf{V}=-\mathbf{T}-\mathbf{\omega}\times\mathbf{P}$.

where

• $\mathbf{P}$ is a point in the scene where Z is the distance to that scene point.
• $\mathbf{V}$ is the relative motion between the camera and the scene,
• $\mathbf{T}$ is the translational component of the motion, and
• $\mathbf{\omega}$ is the angular velocity of the motion.

Relation to optical flow

Main article: optical flow

The motion field is an ideal construction, based on the idea that it is possible to determine the motion of each image point, and above it is described how this 2D motion is related to 3D motion. In practice, however, the true motion field can only be approximated based on measurements on image data. The problem is that in most cases each image point has an individual motion which therefore has to be locally measured by means of a neighborhood operation on the image data. As consequence, the correct motion field cannot be determined for certain types of neighborhood and instead an approximation, often referred to as the optical flow, has to be used. For example, a neighborhood which has a constant intensity may correspond to a non-zero motion field, but the optical flow is zero since no local image motion can be measured. Similarly, a neighborhood which is intrinsic 1-dimensional (for example, an edge or line) can correspond to an arbitrary motion field, but the optical flow can only capture the normal component of the motion field. There are also other effects, such as image noise, 3D occlusion, temporal aliasing, which are inherent to any method for measuring optical flow and causes the resulting optical flow deviate from the true motion field.

In short, the motion field cannot be correctly measured for all image points, and the optical flow is an approximation of the motion field. There are several different ways to compute the optical flow based on different criteria of how an optical estimation should be made.

References

• Bernd Jähne and Horst Haußecker (2000). Computer Vision and Applications, A Guide for Students and Practitioners. Academic Press. ISBN 0-13-085198-1. 

• Linda G. Shapiro and George C. Stockman (2001). Computer Vision. Prentice Hall. ISBN 0-13-030796-3. 

• Milan Sonka, Vaclav Hlavac and Roger Boyle (1999). Image Processing, Analysis, and Machine Vision. PWS Publishing. ISBN 0-534-95393-X.