Introduction to mathematics of general relativity

An understanding of calculus and differential equations is necessary for the understanding of nonrelativistic physics. In order to understand special relativity one also needs an understanding of tensor calculus. To understand the general theory of relativity, one needs a basic introduction to the mathematics of curved spacetime that includes a treatment of curvilinear coordinates, nontensors, curved space, parallel transport, Christoffel symbols, geodesics, covariant differentiation, the curvature tensor, Bianchi identity, and the Ricci tensor. This article follows the basic treatment in the lecture series on the topic, intended for advanced undergraduates, given by Paul Dirac at Florida State University. (Dirac 1996)

All the mathematics discussed in this article were known before Einstein's general theory of relativity.

For an introduction based on the specific physical example of particles orbiting a large mass in circular orbits, see Newtonian motivations for general relativity for a nonrelativistic treatment and Theoretical motivation for general relativity for a fully relativistic treatment.

Mathematics of special relativity

Vectors

Interval between two points

Spacetime physics requires four coordinates for the description of a point in spacetime:

:$ct=x^0\; quad\; x=x^1\; quad\; y=x^2\; quad\; z=x^3$

where c is the speed of light and x, y, and z are spatial coordinates.

A point very close to our original point is

:$x^\{mu\}\_\{\; \}\; +\; dx^\{mu\}\; quad\; mu\; in\; \{\; 0,1,2,3\}$.

The square of the distance, or interval, between the two points is

:$ds^2\; =\; -left\; (\; dx^\{0\}\; ight\; )\; ^2\; +\; left\; (\; dx^\{1\}\; ight\; )\; ^2\; +\; left\; (\; dx^\{2\}\; ight\; )\; ^2+\; left\; (\; dx^\{3\}\; ight\; )\; ^2$

and is invariant under coordinate transformations. Here we are using the Minkowski metric.

Coordinate transformations

Transformation of dx

If one defines a new coordinate system $x^\{mu\text{'}\}$ such that

:$x^\{mu\text{'}\}\; =\; x^\{mu\text{'}\}left\; (\; x^\{mu\}\; ight\; )$

then

:$dx^\{mu\text{'}\}\; =\; \{\; partial\; x^\{mu\text{'}\}\; over\; partial\; x^\{\; u\}\; \}\; dx^\{\; u\}\; stackrel\{mathrm\{def\{=\}\; \{x^\{mu\text{'}\_\{,\; u\}\; ;\; dx^\{\; u\}$

where repeated indices are summed according to the Einstein summation convention.

The comma in the subscript of the last term indicates differentiation.

Transformation of a scalar

A scalar quantity transforms as

:$\{partial\; f\; left\; (\; x^\{mu\}\; ight\; )\; over\; partial\; x^\{mu\text{'}\}\; \}\; =\; \{partial\; x^\{\; u\}\; over\; partial\; x^\{mu\text{'}\}\; \}\; \{partial\; f\; left\; (\; x^\{mu\}\; ight\; )\; over\; partial\; x^\{\; u\}\; \}\; =\; \{x^\{\; u\_\{,\; mu\text{'}\}\; \{partial\; f\; left\; (\; x^\{mu\}\; ight\; )\; over\; partial\; x^\{\; u\}\; \}$.

Contravariant vectors

Quantities $A^\{mu\}$ that transform in the same way as $dx^\{mu\}$ under a change of coordinates,

:$A^\{mu\text{'}\}\; =\; \{x^\{mu\text{'}\_\{,\; u\}\; ;\; A^\{\; u\}$,

form a contravariant vector. The squared length of the vector is the invariant quantity

:$(A,A)\; stackrel\{mathrm\{def\{=\}\; -left\; (\; A^\{0\}\; ight\; )\; ^2\; +\; left\; (\; A^\{1\}\; ight\; )\; ^2\; +\; left\; (\; A^\{2\}\; ight\; )\; ^2+\; left\; (\; A^\{3\}\; ight\; )\; ^2$.

The term on the left is the notation for the inner product of A with itself.

Covariant vectors

The covariant vector is defined as

:$A\_0\; stackrel\{mathrm\{def\{=\}\; -A^0\; quad\; A\_1\; stackrel\{mathrm\{def\{=\}\; A^1\; quad\; A\_2\; stackrel\{mathrm\{def\{=\}\; A^2\; quad\; A\_3\; stackrel\{mathrm\{def\{=\}\; A^3$.

It transforms as

:$A\_\{mu\text{'}\}\; =\; x^\{\; u\}\_\{,\; mu\text{'}\}\; A\_\{\; u\}$.

Inner product

The inner product of two vectors is written

:$(A,B)\_\{\; \}^\{\; \}\; =\; A\_\{mu\}B^\{mu\}\; =\; B\_\{mu\}A^\{mu\}$.

This quantity is also invariant under coordinate transformations.

Tensors

Definition

A rank-2 contravariant tensor can be constructed from the outer product of vectors as

:$T^\{mu\; u\}\; stackrel\{mathrm\{def\{=\}\; A^\{mu\}B^\{\; u\}\; +\; C^\{mu\}D^\{\; u\}\; +\; E^\{mu\}F^\{\; u\}\; +\; cdots$.

Contravariant tensor

The components of a rank 2 contravariant tensor transform in the same way as the quantities $\{A^\{mu\}B^\{\; u\_\{\; \}^\{\; \}$,

:$T^\{mu\text{'}\; u\text{'}\}=\{x^\{mu\text{'}\_\{,mu\}\; ;\; \{x^\{\; u\text{'}\_\{,\; u\}\; ;\; T^\{mu\; u\}$

Covariant and mixed tensors

Higher rank tensors are constructed similarly as are covariant and mixed tensors. For a rank 2 covariant tensor, the transformation is

:$T\_\{mu\text{'}\; u\text{'}\}=\{x^\{mu\_\{,\; mu\text{'}\}\; ;\; \{x^\{\; u\_\{,\; u\text{'}\}\; ;\; T\_\{mu\; u\}$.

Oblique axes

The interval and the metric tensor

An oblique coordinate system is one in which the axis are not necessarily orthogonal to each other. For oblique axes, the interval is

:$\{ds^2\}\_\{\; \}^\{\; \}\; =\; g\_\{mu\; u\}dx^\{mu\}dx^\{\; u\}\; =\; g\_\{\; u\; mu\}dx^\{mu\}dx^\{\; u\}$

where the coefficients $g\_\{mu\; u\}$, called the metric tensor depend on the system of oblique axes.

Determinant of the metric tensor

The determinant of $g\_\{mu\; u\}$ is denoted $g$ and is always negative for any real coordinate axes.

Inner product

The inner product of any two vectors

:$\{(A,B)\}\_\{\; \}^\{\; \}\; =\; g\_\{mu\; u\}A^\{mu\}B^\{\; u\}$

is invariant.

Relation between covariant and contravariant tensors

Covariant tensors can be converted to and from contravariant tensors by

:$\{A\_\{mu\_\{\; \}^\{\; \}\; =\; g\_\{mu\; u\}A^\{\; u\}$

and

:$\{A^\{mu\_\{\; \}^\{\; \}\; =\; g^\{mu\; u\}A\_\{\; u\}$

where $g^\{mu\; u\}$ is the cofactor of the corresponding $g\_\{mu\; u\}$

and

:.

Nontensors

A nontensor is a tensor-like quantity $\{N\_\{mu$ that behaves like a tensor in the raising and lowering of indices,

:$\{N\_\{mu\_\{\; \}^\{\; \}\; =\; g\_\{mu\; u\}N^\{\; u\}$

and

:$\{N^\{mu\_\{\; \}^\{\; \}\; =\; g^\{mu\; u\}N\_\{\; u\}$,

but that does not transform like a tensor under a coordinate transformation.

Mathematics of general relativity

Curvilinear coordinates and curved spacetime

Curvilinear coordinates are coordinates in which the angles between axes can change from point-to-point. In other words, the metric tensor $g\_\{mu\; u\}$ in curvilinear coordinates is no longer a constant, but depends upon the spacetime location of the metric tensor. The metric tensor is therefore a field quantity.

Like the surface of a ball embedded in three-dimensional space, we can imagine four-dimensional spacetime as embedded in a flat space of a higher dimension. The coordinates on the surface of the ball are curvilinear, while the coordinates in three-dimensional space can be rectilinear. While the coordinates of four-dimensional, curved spacetime are curvilinear; the coordinates of four-dimensional spacetime are embedded in a larger, N-dimensional space of rectilinear (flat) coordinates.

Parallel transport

---

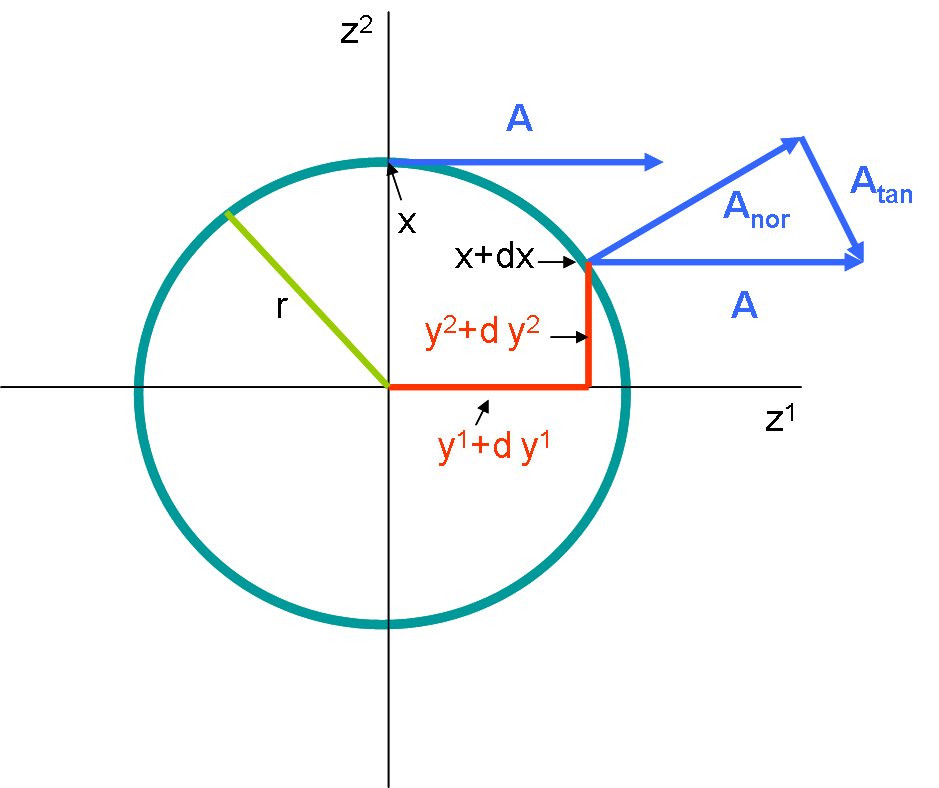
thumb|450px|right|Example: Parallel displacement along a circle of a three-dimensional ball embedded in two dimensions. The circle of radius r is embedded in a two-dimensional space characterized by the coordinates ">$z^1$ and $z^2$. The circle itself is characterized by coordinates $y^1$ and $y^2$ in the two dimensional space. The circle itself is one-dimensional and can be characterized by its arc length x. The coordinate y is related to the coordinate x through the relation $y^1\; =\; r\; sin(\; x\; /\; r)$ and $y^2\; =\; r\; cos(\; x\; /\; r)$. This gives $partial\; y^1\; /\; partial\; x\; =\; cos(\; x\; /\; r)$

and

$partial\; y^2\; /\; partial\; x\; =\; -\; sin(\; x\; /\; r)$.

In this case the metric is a scalar and is given by

$g\; =\; cos^2(\; x\; /\; r)\; +\; sin^2(x/r)\; =\; 1$.

The interval is then

$ds^2\; =\; g\; dx^2\; =\; dx^2$.

The interval is just equal to the arc length as expected.

The interval in a high dimensional space

Imagine our four-dimensional, curved spacetime is embedded in a larger N dimensional flat space. Any true physical vector lies entirely in the curved physical space. In other words, the vector is tangent to the curved physical spacetime. It has no component normal to the four-dimensional, curved spacetime.

In the N dimensional flat space with coordinates $z^n\; (n=1,2,3,cdots\; ,\; N\; )$ the interval between neighboring points is

:$ds^2\_\{\; \}\; =\; eta\_\{nm\}\; dz^n\; dz^m$

where $eta\_\{nm\}$ is the metric for the flat space. We do not assume the coordinates are orthogonal, only rectilinear.

The relation between neighboring contravariant vectors: Christoffel symbols

The difference in $y!$ for two neighboring points in the surface differing by $d\; x^\{mu\}!$ is

:$d\; y^\{n\}\; =\; \{y^n\}\_\{,mu\}\; d\; x^\{mu\}$

where

:$\{y^n\}\_\{,mu\}\; =\; \{partial\; y^n(x)\; over\; partial\; x^\{mu\}\; \}.$

The interval between two neighboring points in physical spacetime becomes

:$ds^2\_\{\; \}\; =\; eta\_\{nm\}\; dy^n\; dy^m\; =\; eta\_\{nm\}\; \{y^n\}\_\{,mu\}\; \{y^m\}\_\{,\; u\}\; dx^\{mu\}\; dx^\{\; u\}\; =\; g\_\{mu\; u\}\; d\; x^\{mu\}\; d\; x^\{\; u\}$

where

:$g\_\{mu\; u\}\; =\; eta\_\{nm\}\; \{y^n\}\_\{,mu\}\; \{y^m\}\_\{,\; u\}.$

A contravariant vector at a point x in physical spacetime is related to the same contravariant vector at the same point $y(x)$ in N-dimensional space by the relation

:$A^\{n\}\; =\; \{y^n\}\_\{,mu\}\; A^\{mu\}.$

The vector lies in the surface of physical spacetime.

Now shift the vector $A^\{n\}!$ to the point $y^n(x+dx)!$ keeping it parallel to itself. In other words, we hold the components of the vector constant during the shift. The vector no longer lies in the surface because of curvature of the surface.

The shifted vector can be split into two parts, one tangent to the surface and one normal to surface, as

:$A^\{n\}\; =\; A^\{n\}\_\{mathrm\{tan\; +\; A^\{n\}\_\{mathrm\{nor$.

Let $K^\{mu\}\; !$ be the components of $A^\{n\}\_\{mathrm\{tan$ in the "x" coordinate system. This transformation is given by:

:$A^\{n\}\_\{mathrm\{tan\; =\; K^\{mu\}\; \{y^n\}\_\{,mu\}\; (x+dx)$.

The normal vector $A^\{n\}\_\{mathrm\{nor$ is normal to every vector in the surface including the unit vectors that define the components of $x^\{mu\}$. Therefore

:$A^\{n\}\_\{mathrm\{nor\; ;\; ;\; y\_\{n,mu\}\; (x+dx)\; =\; 0$.

This allows us to write

:$A^\{n\}\; ;\; y\_\{n,mu\}\; (x+dx)\; =\; K^\{\; u\}\; g\_\{mu\; u\}(x+dx)$

or

:$K\_\{\; u\}\; -\; A\_\{\; u\}\; stackrel\{mathrm\{def\{=\}\; dA\_\{\; u\}\; =\; A^\{mu\}\; ;\; \{y^n\}\_\{,mu\}\; y\_\{n,\; u,\; sigma\}\; dx^\{sigma\}\; stackrel\{mathrm\{def\{=\}\; A^\{mu\}\; ;\; Gamma\_\{mu\; u\; sigma\}\; dx^\{sigma\}$

where

:$Gamma\_\{mu\; u\; sigma\}\; stackrel\{mathrm\{def\{=\}\; \{y^n\}\_\{,mu\}\; y\_\{n,\; u,\; sigma\}$

is a nontensor called the Christoffel symbol of the first kind. It can be shown to be related to the metric tensor through the relation

:$Gamma\_\{mu\; u\; sigma\}\; =\; \{1\; over\; 2\}\; left\; (\; g\_\{mu\; u\; ,\; sigma\}\; +\; g\_\{mu\; sigma\; ,\; u\}\; -\; g\_\{\; u\; sigma\; ,\; mu\}\; ight\; )$.

Since the Christoffel symbol can be written entirely in terms of the metric in physical spacetime, all reference to the N-dimensional space has disappeared.

Christoffel symbol of the second kind

The Christoffel symbol of the second kind is defined as

:$Gamma^\{mu\}\_\{\; u\; sigma\}\; stackrel\{mathrm\{def\{=\}\; g^\{mu\; lambda\}\; Gamma\_\{lambda\; u\; sigma\}$.

This operation is allowed for nontensors.

This allows us to write

:$dA\_\{\; u\}\; =\; A\_\{mu\}\; Gamma^\{mu\}\_\{\; u\; sigma\}\; dx^\{sigma\}$

and

:$dA^\{\; u\}\; =\; -A^\{mu\}\; Gamma^\{\; u\}\_\{\; mu\; sigma\}\; dx^\{sigma\}$.

The minus sign in the second expression can be seen from the invariance of an inner product of two vectors

:$dleft\; (\; A^\{\; u\}\; B\_\{\; u\}\; ight\; )\; =\; 0$.

The constancy of the length of the parallel displaced vector

From Dirac:

:

The constancy of the length of the vector follows from geometrical arguments. When we split up the vector into tangential and normal parts ... the normal part is infinitesimal and is orthogonal to the tangential part. It follows that, to the first order, the length of the whole vector equals that of its tangential part.

The covariant derivative

The partial derivative of a vector with respect to a spacetime coordinate is composed of two parts, the normal partial derivative minus the change in the vector due to parallel transport

:$A\_\{mu\; ;\; u\}\; =\; A\_\{mu\; ,\; u\}\; -\; A\_\{alpha\}\; Gamma^\{alpha\}\_\{\; mu\; u\}.$

It is relatively easy to prove that the metric tensor $g\_\{ij\},$ is covariantly constant, i.e. $g\_\{ij;k\}=0,$ for any choice of $i,j,k$.

The covariant derivative of a product is:$left(A\; B\; ight)\_\{;sigma\}=left(A\_\{;sigma\}\; ight\; )B\; +\; Aleft(B\_\{;sigma\}\; ight)$

that is, the covariant derivative satisfies the product rule (due to Gottfried Leibniz).

Geodesics

Suppose we have a point $z^\{mu\}$ that moves along a track in physical spacetime. Suppose the track is parameterized with the quantity $au$. The "velocity" vector that points in the direction of motion in spacetime is

:$u^\{mu\}\; =\; \{\; dz^\{mu\}\; over\; d\; au\; \}.$

The variation of the velocity upon parallel displacement along the track is then

:$\{\; d\; u^\{\; u\}\; over\; d\; au\}\; +\; Gamma^\{\; u\}\_\{mu\; sigma\}\; u^\{mu\}\; u^\{sigma\}.$

If there are no "forces" acting on the point, then the velocity is unchanged along the track and we have

:$\{\; d\; u^\{\; u\}\; over\; d\; au\}\; +\; Gamma^\{\; u\}\_\{mu\; sigma\}\; u^\{mu\}\; u^\{sigma\}\; quad\; =\; quad\; \{\; d^2\; z^\{\; u\}\; over\; d\; au^2\}\; +\; Gamma^\{\; u\}\_\{mu\; sigma\}\; \{\; d\; z^\{mu\}\; over\; d\; au\}\; \{\; d\; z^\{sigma\}\; over\; d\; au\}\; quad\; =\; quad\; 0,$

which is called the geodesic equation.

Curvature tensor

Definition

The curvature K of a surface is simply the angle through which a vector is turned as we take it around an infinitesimal closed path. For a two dimensional Euclidean surface we have

:$delta\; heta\; =\; mbox\{(Area\; enclosed)\}\; cdot\; K$.

For a triangle on a spherical surface the angle is the excess (over 180 degrees) of the sum of the angles of the triangle. For a spherical surface of radius r, the curvature is

:$K\; =\; \{1\; over\; r^2\}$.

The definition of curvature generalizes to

:

where $A^\{mu\}!$ is an arbitrary vector transported around a closed loop of area $Delta^\{\; ho\; sigma\}!$ along the $x^\{\; ho\}!$ and $x^\{sigma\}!$ directions. Here,

:$Delta^\{\; ho\; sigma\}\; stackrel\{mathrm\{def\{=\}\; dx^\{\; ho\}\; dx^\{sigma\}!.$

This expression can be reduced to the commutation relation

:

where

:.

In flat spacetime, the derivatives commute and the curvature is zero.

ymmetries of the curvature tensor

The curvature tensor is antisymmetric in the last two indices

:.

Also

:

:$R\_\{mu\; u\; ho\; sigma\}^\{\; \}\; =\; -R\_\{\; u\; mu\; ho\; sigma\}$

and

:$R\_\{mu\; u\; ho\; sigma\}^\{\; \}\; =\; R\_\{\; ho\; sigma\; mu\; u\; \}\; =\; R\_\{\; sigma\; ho\; u\; mu\; \}$.

A consequence of the symmetries is that the curvature tensor has only 20 independent components.

Bianchi identity

The following differential relation, known as the Bianchi identity is true.

:$\{R^\{\; u\_\{mu\; ho\; sigma\; ;\; au\}\; +\; \{R^\{\; u\_\{mu\; sigma\; au\; ;\; ho\; \}\; +\; \{R^\{\; u\; \_\{mu\; au\; ho\; ;\; sigma\; \}\; =\; 0$

Ricci tensor and scalar curvature

The Ricci tensor is defined as the contraction

:$R\_\{\; u\; ho\}\; stackrel\{mathrm\{def\{=\}\; \{R^\{mu\_\{\; umu\; ho\}$.

A second contraction yields the scalar curvature

:$R\; stackrel\{mathrm\{def\{=\}\; g^\{\; u\; ho\}\; R\_\{\; u\; ho\}\; =\; \{R^\{\; u\_\{\; u\}$.

It can be shown that consequence of the Bianchi identity is

:$2\{R^\{alpha\_\{sigma\; ;\; alpha\}\; -\; R\_\{;sigma\}\; =\; 0$.

ee also

*Riemannian geometry
*Differential geometry and topology
*List of differential geometry topics
*General Relativity

References

*
*
*
*
*