Coastline paradox

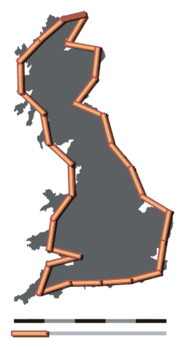
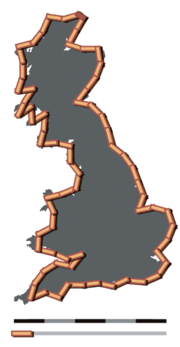
An example of the coastline paradox. If the coastline of Great Britain is measured using fractal units 100 km (62 mi) long, then the length of the coastline is approximately 2,800 km (1,700 mi). With 50 km (31 mi) units, the total length is approximately 3,400 km (2,100 mi), approximately 600 km (370 mi) longer.

The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal-like properties of coastlines.^[1][2] It was first observed by Lewis Fry Richardson.

More concretely, the length of the coastline depends on the method used to measure it. Since a landmass has features at all scales, from hundreds of kilometers in size to tiny fractions of a millimeter and below, there is no obvious limit to the size of the smallest feature that should not be measured around, and hence no single well-defined perimeter to the landmass. Various approximations exist when specific assumptions are made about minimum feature size.

For practical considerations, an appropriate choice of minimum feature size is on the order of the units being used to measure. If a coastline is measured in kilometers, then small variations much smaller than one kilometer are easily ignored. To measure the coastline in centimeters, tiny variations of the size of centimeters must be considered. However, at scales on the order of centimeters various arbitrary and non-fractal assumptions must be made, such as where an estuary joins the sea, or where in a broad tidal flat the coastline measurements ought to be taken.

Extreme cases of the coastline paradox include the fjord-heavy coastlines of Norway, Chile and the Pacific Northwest of North America. From the southern tip of Vancouver Island northwards to the southern tip of the Alaska Panhandle, the convolutions of the coastline of the Canadian province of British Columbia make it over 10% of the entire Canadian coastline—25,725 km (15,985 mi) vs 243,042 km (151,019 mi)^{[clarification needed]} over a linear distance of only 965 km (600 mi), including the maze of islands of the Arctic archipelago.^[3]

See also

• How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension
• Fractal dimension
• Paradox of the Heap

Notes

1. ^ Weisstein, Eric W., "Coastline Paradox" from MathWorld.
2. ^ Mandelbrot, Benoit (1983). The Fractal Geometry of Nature. W.H. Freeman and Co.. 25–33. ISBN 978-0-7167-1186-5. 
3. ^ Sebert, L.M., and M. R. Munro. 1972. Dimensions and Areas of Maps of the National Topographic System of Canada. Technical Report 72-1. Ottawa: Department of Energy, Mines and Resources, Surveys and Mapping Branch.

External links

• The Atlas of Canada – Coastline and Shoreline
• La costa infinita (animation of a coastline with fractal details)