Paris' law

Schematic plot of the typical relationship between the crack growth rate and the range of the stress intensity factor. In practice, the Paris law is calibrated to model the linear interval around the center.

Paris' law (also known as the Paris-Erdogan law) relates the stress intensity factor range to sub-critical crack growth under a fatigue stress regime. As such, it is the most popular fatigue crack growth model used in materials science and fracture mechanics. The basic formula reads^[1]

$\frac{{\rm d}a}{{\rm d}N} = C \Delta K^m$,

where a is the crack length and N is the number of load cycles. Thus, the term on the left side, known as the crack growth rate,^[2] denotes the infinitesimal crack length growth per increasing number of load cycles. On the right hand side, C and m are material constants, and ΔK is the range of the stress intensity factor, i.e., the difference between the stress intensity factor at maximum and minimum loading

ΔK = K_max − K_min,

where K_max is the maximum stress intensity factor and K_min is the minimum stress intensity factor.^[3]

History and use

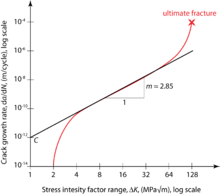
The formula was introduced by P.C. Paris in 1961.^[4] Being a power law relationship between the crack growth rate during cyclic loading and the range of the stress intensity factor, the Paris law can be visualized as a linear graph on a log-log plot, where the x-axis is denoted by the range of the stress intensity factor and the y-axis is denoted by the crack growth rate.

Paris' law can be used to quantify the residual life (in terms of load cycles) of a specimen given a particular crack size. Defining the crack intensity factor as

$K=\sigma Y \sqrt{\pi a}$,

where σ is a uniform tensile stress perpendicular to the crack plane and Y is a dimensionless parameter that depends on the geometry, the range of the stress intensity factor follows as

$\Delta K=\Delta\sigma Y \sqrt{\pi a}$,

where Δσ is the range of cyclic stress amplitude. Y takes the value 1 for a center crack in an infinite sheet. The remaining cycles can be found by substituting this equation in the Paris law

$\frac{{\rm d}a}{{\rm d}N} = C \Delta K^m =C(\Delta\sigma Y \sqrt{\pi a})^m$.

For relatively short cracks, Y can be assumed as independent of a and the differential equation can be solved via separation of variables

$\int^{N_f}_0 {\rm d}N = \int^{a_c}_{a_i}\frac{{\rm d}a}{C(\Delta\sigma Y \sqrt{\pi a})^m } =\frac{1}{C(\Delta\sigma Y \sqrt{\pi})^m }\int^{a_c}_{a_i} a^{-\frac{m}{2}}\;{\rm d}a$

and subsequent integration

$N_f=\frac{2\;(a_c^{\frac{2-m}{2}}-a_i^{\frac{2-m}{2}})}{(2-m)\;C(\Delta\sigma Y \sqrt{\pi})^m}$,

where N_f is the remaining number of cycles to fracture, a_c is the critical crack length at which instantaneous fracture will occur, and a_i is the initial crack length at which fatigue crack growth starts for the given stress range Δσ. If Y strongly depends on a, numerical methods might be required to find reasonable solutions.

For the application to adhesive joints in composites, it is more useful to express the Paris Law in terms of fracture energy rather than stress intensity factors.^[5]

References

1. ^ "The Paris law". Fatigue crack growth theory. University of Plymouth. http://www.tech.plym.ac.uk/sme/tutorials/FMTut/Fatigue/FatTheory1.htm. Retrieved 21 June 2010. 
2. ^ M. Ciavarella, N. Pugno (14–17 September 2005). "A generalized law for fatigue crack growth" (PDF). XXXIV Convegno Nazionale. Associazione Italiana per l'analisi delle sollecitazioni. http://www.aiasonline.org/AIAS2005/Articoli/art007.pdf. Retrieved 21 July 2010. 
3. ^ Roylance, David (1 May 2001). "Fatigue" (PDF). Department of Materials Science and Engineering, Massachusetts Institute of Technology. http://ocw.mit.edu/courses/materials-science-and-engineering/3-11-mechanics-of-materials-fall-1999/modules/fatigue.pdf. Retrieved 23 July 2010. 
4. ^ P.C. Paris, M.P. Gomez, and W.E. Anderson. A rational analytic theory of fatigue. The Trend in Engineering, 1961, 13: p. 9-14.
5. ^ Wahab, M.M.A., I.A. Ashcroft, A.D. Crocombe, and P.A. Smith, Fatigue crack propagation in adhesively bonded joints. Key Engineering Materials, 2003, 251-252: p. 229-234