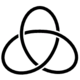
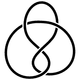
- Chiral knot
-
In the mathematical field of knot theory, a chiral knot is a knot that is not equivalent to its mirror image. An oriented knot that is equivalent to its mirror image is an amphichiral knot, also called an achiral knot or amphicheiral knot. The chirality of a knot is a knot invariant. A knot's chirality can be further classified depending on whether or not it is invertible.
Contents
Background
The chirality of certain knots was long suspected, and was proven by Max Dehn in 1914. P. G. Tait conjectured that all amphichiral knots had even crossing number, but a counterexample was found by Morwen Thistlethwaite et al. in 1998.[1] However, Tait's conjecture was proven true for prime, alternating knots.[2]
Number of knots of each type of chirality for each crossing number Number of crossings 3 4 5 6 7 8 9 10 11 12 13 14 15 16 OEIS sequence Chiral knots 1 0 2 2 7 16 49 152 552 2118 9988 46698 253292 1387166 N/A Reversible knots 1 0 2 2 7 16 47 125 365 1015 3069 8813 26712 78717 A051769 Fully chiral knots 0 0 0 0 0 0 2 27 187 1103 6919 37885 226580 1308449 A051766 Amphichiral knots 0 1 0 1 0 5 0 13 0 58 0 274 1 1539 A052401 Positive Amphichiral knots 0 0 0 0 0 0 0 0 0 1 0 6 0 65 A051767 Negative Amphichiral knots 0 0 0 0 0 1 0 6 0 40 0 227 1 1361 A051768 Fully Amphichiral knots 0 1 0 1 0 4 0 7 0 17 0 41 0 113 A052400 Chiral knot
- Both possible trefoil knots.
-
The left-handed trefoil knot.
-
The right-handed trefoil knot.
The simplest chiral knot is the trefoil knot, which was shown to be chiral by Max Dehn. All torus knots are chiral. The Alexander polynomial cannot detect the chirality of a knot, but the Jones polynomial can in some cases; if Vk(q) ≠ Vk(q−1), then the knot is chiral, however the converse is not true. The HOMFLY polynomial is even better at detecting chirality, but no knot invariant is known which can fully detect chirality.[3]
Reversible knot
A chiral knot that is invertible is classified as a reversible knot.[4]
Fully chiral knot
If a knot is not equivalent to its inverse or its mirror image, it is a fully chiral knot.[4]
Amphichiral knot
The figure eight knot is the simplest amphichiral knot.
An amphichiral knot is one which has an orientation-reversing self-homeomorphism of the 3-sphere, α, fixing the knot set-wise. All amphichiral alternating knots have even crossing number. The only known amphichiral knot with odd crossing number is a 15-crossing knot discovered by Hoste et al.[2]
Fully amphichiral
If a knot is isotopic to both its reverse and its mirror image, it is fully amphichiral. The simplest knot with this property is the figure eight knot.
Positive amphichiral
If the self-homeomorphism, α, preserves the orientation of the knot, it is said to be positive amphichiral. This is equivalent to the knot being isotopic to its mirror. No knots with crossing number smaller than twelve are positive amphichiral.[4]
Negative amphichiral
The first negative amphichiral knot.If the self-homeomorphism, α, reverses the orientation of the knot, it is said to be negative amphichiral. This is equivalent to the knot being isotopic to the reverse of its mirror image. The knot with this property that has the fewest crossings is the knot 817.[4]
References
- ^ History of Knot Theory and Certain Applications of Knots and Links
- ^ a b Weisstein, Eric W. "Amphichiral Knot." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/AmphichiralKnot.html
- ^ http://arxiv.org/pdf/hep-th/9401095.pdf
- ^ a b c d Three Dimensional Invariants - Knot Atlas
See also
Categories:
Wikimedia Foundation. 2010.
