Braid theory

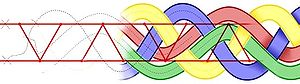The braid is associated with a planar graph.

The 24 elements of a permutation group on 4 elements as braids. Note that all crossings shown are of the left-over-right sort and other choices are possible. Indeed, the braid group on two or more strands is infinite.

In topology, a branch of mathematics, braid theory is an abstract geometric theory studying the everyday braid concept, and some generalizations. The idea is that braids can be organized into groups, in which the group operation is 'do the first braid on a set of strings, and then follow it with a second on the twisted strings'. Such groups may be described by explicit presentations, as was shown by Emil Artin (1947). For an elementary treatment along these lines, see the article on braid groups. Braid groups may also be given a deeper mathematical interpretation: as the fundamental group of certain configuration spaces.

Braids as fundamental groups

To explain how to reduce a braid group in the sense of Artin to a fundamental group, we consider a connected manifold X of dimension at least 2. The symmetric product of n copies of X means the quotient of Xⁿ, the n-fold Cartesian product of X with itself, by the permutation action of the symmetric group on n letters operating on the indices of coordinates. That is, an ordered n-tuple is in the same orbit as any other that is a re-ordered version of it.

A path in the n-fold symmetric product is the abstract way of discussing n points of X, considered as an unordered n-tuple, independently tracing out n strings. Since we must require that the strings never pass through each other, it is necessary that we pass to the subspace Y of the symmetric product, of orbits of n-tuples of distinct points. That is, we remove all the subspaces of Xⁿ defined by conditions x_i = x_j. This is invariant under the symmetric group, and Y is the quotient by the symmetric group of the non-excluded n-tuples. Under the dimension condition Y will be connected.

With this definition, then, we can call the braid group of X with n strings the fundamental group of Y (for any choice of base point – this is well-defined up to isomorphism). The case where X is the Euclidean plane is the original one of Artin. In some cases it can be shown that the higher homotopy groups of Y are trivial.

Closed braids

When X is the plane, the braid can be closed, i.e., corresponding ends can be connected in pairs, to form a link, i.e., a possibly intertwined union of possibly knotted loops in three dimensions. The number of components of the link can be anything from 1 to n, depending on the permutation of strands determined by the link. A theorem of J. W. Alexander demonstrates that every link can be obtained in this way as the "closure" of a braid. Compare with string links.

Different braids can give rise to the same link, just as different crossing diagrams can give rise to the same knot. Markov (1935) describes two moves on braid diagrams that yield equivalence in the corresponding closed braids. A single-move version of Markov's theorem, was published by Lambropoulou & Rourke (1997).

Vaughan Jones originally defined his polynomial as a braid invariant and then showed that it depended only on the class of the closed braid.

Applications

Braid theory has recently been applied to fluid mechanics, specifically to the field of chaotic mixing in fluid flows. The braiding of (2+1) dimensional space-time trajectories formed by motion of physical rods, periodic orbits or "ghost rods", and almost-invariant sets has been used to estimate the topological entropy of several engineered and naturally occurring fluid systems, via the use of Nielsen–Thurston classification.^[1]

See also

• Braid group
• Knot theory
• Braided monoidal category
• Change ringing software – how software uses braid theory to model bell-ringing patterns

Notes

1. ^ Boyland, Aref & Stremler (2000); Gouillart & Thiffeault (2006); Stremler et al. (2011).

References

• Artin, Emil (1947), "Theory of braids", Annals of Mathematics, 2nd Ser. 48 (1): 101–126, doi:10.2307/1969218, JSTOR 1969218, MR0019087 .
• Birman, Joan S. (1974), Braids, links, and mapping class groups, Annals of Mathematics Studies, 82, Princeton, N.J.: Princeton University Press, ISBN 9780691081496, MR0375281 .
• Boyland, Philip L.; Aref, Hassan; Stremler, Mark A. (2000), "Topological fluid mechanics of stirring", Journal of Fluid Mechanics 403: 277–304, Bibcode 2000JFM...403..277B, doi:10.1017/S0022112099007107, MR1742169, http://www.math.ufl.edu/~boyland/stir.pdf .
• Fox, R.; Neuwirth, L. (1962), "The braid groups", Mathematica Scandinavica 10: 119–126, MR0150755 .
• Gouillart, Emmanuelle; Thiffeault, Jean-Luc; Finn, Matthew D. (2006), "Topological mixing with ghost rods", Physical Review E. Statistical, Nonlinear, and Soft Matter Physics 73 (3): 036311, arXiv:nlin/0510075, doi:10.1103/PhysRevE.73.036311, MR2231368 .
• Lambropoulou, Sofia; Rourke, Colin P. (1997), "Markov's theorem in 3-manifolds", Topology and its Applications 78 (1–2): 95–122, doi:10.1016/S0166-8641(96)00151-4, MR1465027 .
• Markov, Andrey (1935), "Über die freie Äquivalenz der geschlossenen Zöpfe" (in German), Recueil Mathématique De La Société Mathématique De Moscou 1: 73–78, http://mi.mathnet.ru/msb5359 .
• Stremler, Mark A.; Ross, Shane D.; Grover, Piyush; Kumar, Pankaj (2011), "Topological chaos and periodic braiding of almost-cyclic sets", Physical Review Letters 106 (11): 114101, doi:10.1103/PhysRevLett.106.114101 .