Chain (algebraic topology)

This article is about algebraic topology. For the term chain in order theory, see chain (order theory).

In algebraic topology, a simplicial k-chain is a formal linear combination of k-simplices.^[1]

Integration on chains

Integration is defined on chains by taking the linear combination of integrals over the simplices in the chain with coefficients typically integers. The set of all k-chains forms a group and the sequence of these groups is called a chain complex.

Boundary operator on chains

The boundary of a polygonal curve is a linear combination of its nodes; in this case, some linear combination of A₁ through A₆. Assuming the segments all are oriented left-to-right (in increasing order from A_k to A_k+1), the boundary is A₆ − A₁.

A closed polygonal curve, assuming consistent orientation, has null boundary.

The boundary of a chain is the linear combination of boundaries of the simplices in the chain. The boundary of a k-chain is a (k−1)-chain. Note that the boundary of a simplex is not a simplex, but a chain with coefficients 1 or −1 – thus chains are the closure of simplices under the boundary operator.

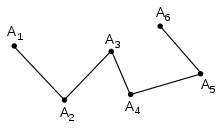
Example 1: The boundary of a path is the formal difference of its endpoints: it is a telescoping sum. To illustrate, if the 1-chain $c = t_1 + t_2 + t_3\,$ is a path from point $v_1\,$ to point $v_4\,$, where $t_1=[v_1, v_2]\,$, $t_2=[v_2, v_3]\,$ and $t_3=[v_3, v_4]\,$ are its constituent 1-simplices, then

$\begin{align} \partial_1 c &= \partial_1(t_1 + t_2 + t_3)\\ &= \partial_1(t_1) + \partial_1(t_2) + \partial_1(t_3)\\ &= \partial_1([v_1, v_2]) + \partial_1([v_2, v_3]) + \partial_1([v_3, v_4]) \\ &= ([v_2]-[v_1]) + ([v_3]-[v_2]) + ([v_4]-[v_3]) \\ &= [v_4]-[v_1]. \end{align}$

Example 2: The boundary of the triangle is a formal sum of its edges with signs arranged to make the traversal of the boundary counterclockwise.

A chain is called a cycle when its boundary is zero. A chain that is the boundary of another chain is called a boundary. Boundaries are cycles, so chains form a chain complex, whose homology groups (cycles modulo boundaries) are called simplicial homology groups.

Example 3: A 0-cycle is a linear combination of points such that the sum of all the coefficients is 0. Thus, the 0-homology group measures the number of path connected components of the space.

Example 4: The plane punctured at the origin has nontrivial 1-homology group since the unit circle is a cycle, but not a boundary.

In differential geometry, the duality between the boundary operator on chains and the exterior derivative is expressed by the general Stokes' theorem.

References

1. ^ Hatcher, Allen (2002). Algebraic Topology. Cambridge University Press. ISBN 0-521-79540-0. http://www.math.cornell.edu/~hatcher/AT/ATpage.html.